Внутренние противоречия (неклассические проблемы)

Нелинейность. Включение в лагранжиан эл.-магн. поля неквадратичных по E и В слагаемых ведёт к нелинейной теории. Наиб. известное нелинейное обобщение Э. развито В. Гейзенбергом (W. Heisenberg), Г. Эйлером (Н. Euler), В. Вайскопфом (V. Weisskopf) (1936) и Ю. Швингером (1951) на основе квантово-электродинамич. вычисления поляризации электрон-позитронного вакуума, создаваемой достаточно плавными в пространстве-времени полями, для к-рых удаётся использовать точное решение Дирака уравнения. Соответствующий лагранжиан, для простоты выписываемый в естеств. единицах ( =с= 1),

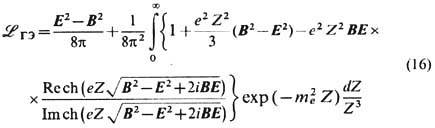
описывает только эл.-магн. поле, причём плавно неоднородное, в пренебрежении производными от инвариантов (3). Он не претендует на самосогласованное "эл.-магн." описание источников поля - электронов и позитронов с зарядами + е и конечной классич. массой т _е, как это предполагалось в нек-рых моделях, напр. М. Борном (М. Born) и Л. Инфельдом (L. Infeld) (1934), выбиравшими лагранжиан в виде

(впрочем, более реалистичном с точки зрения совр. струн теории; Е. С. Фрадкин, А. А. Цейтлин, 1985). Здесь E _макс -нек-рое макс. поле. Мнимая часть (16) характеризует неустойчивость вакуума, точнее, вероятность рождения электрон-позитронных пар в единичном объёме за единицу времени, значительную при и убывающую по закону ехр(-p Е _с/Е )в полях Е<<Е _c. Вещественная часть (16) отвечает за собственную нелинейность "классич." электрон-позитронного вакуума-в отсутствие др. частиц и др. взаимодействий, к-рые, конечно, кардинально меняют ситуацию, скрадывая чисто эл.-магн. взаимодействие, начиная с расстояний ~10^-13 см (сильное) и особенно ~ 10^-16 см (электрослабое).

Если, несмотря на сказанное, обратиться, напр., к модификации закона Кулона, т. е. к сферич. симметрич. решению D = q/r² соответствующих (16) электростатич. ур-ний Максвелла div D =0 (при r 0), , с сингулярностью (точечным зарядом q )в начале координат r = 0, то обнаружится принципиальная роль нелинейности вакуума:

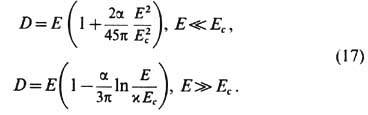
Здесь число учитывает все члены первого порядка по постоянной тонкой структуры Согласно (17), на больших расстояниях поле Е ослабляется по сравнению с g/r²: D/E >1, т. е. поляризов. вакуум экранирует "голый" заряд q. Однако на малых расстояниях эта экранировка уменьшается, и поляризация вакуума меняет знак при На меньших расстояниях возникает антиэкранировка, причём отношение D/E принимает мин. значение a/3pпри

когда ф-ция D(E )достигает максимума и обнаруживающаяся двузначность ф-ции Е(r )делает физически бессмысленным анализ области r<r _мин. Хотя сама квантовая Э. как асимптотическая по a теория вряд ли верна на расстояниях r<<r _мин, апри r~r _мин указанное решение ввиду пространственной неоднородности заведомо выходит за квантово-электродинамич. рамки применимости лагранжиана (16), утверждение о том, что в нелинейной Э. (даже без учёта рождения реальных электрон-позитронных пар) должны существовать макс. электростатич. поле Е _м и аналогичное макс. магнитостатич. поле В _м = В _с ехр (3p/a - 1), представляется неизбежным, поскольку остаётся справедливым и для пространственно однородного поля, напр. в плоском конденсаторе или в соленоиде [М. Гринман (М. Greenman), Ф. Рорлих (F. Rohrlich), 1973; Д. А. Киржниц, А. <Д. Линде, 1978]. Это ещё раз показывает, что наивные представления о точечности заряда, напр. электрона, отвечающие неограниченному при r 0 кулоновскому полю е/r², противоречивы, причём не только в Э., но и в квантовой Э. (Л. Д. Ландау, И. Я. По-меранчук, Е. С. Фрадкин, 1955). Наблюдаемая величина (и масса) заряда так или иначе должна определяться самосогласованными свойствами поляризов. вакуума с учётом неэлектромагн. взаимодействий, "размазывающих" точечный заряд.

Классический размер частиц. При этом в любой, в т. ч. квантовой, теории, отвлекающейся от неэлектромагн. структуры заряда, введение представлений о нелокальном взаимодействии поля с протяжённой заряж. частицей как единым целым наталкивается на значит. трудности, прежде всего причинного характера. В Э., пусть линейной (14), подобные попытки, несмотря на содержательность, также оказываются ограниченными. Среди них наиб. популярно представление о распределении заряда электрона по области размером ~r _е = е ²/т _е с² 3^.10^-13 см ( классический радиус электрона), что соответствует приписыванию, хотя бы частичному, энергии покоя электрона т _е с². его кулоновскому полю. Это представление, конечно, предполагает наличие к.-л. неэлектромагн., упругих сил (т. н. н а т я ж ен и й П у а н к а р е), к-рые препятствуют кулоновскому расталкиванию "частей" электрона и обеспечивают релятивистскую ковариантность его полного 4-импульса, складывающегося из нековариантных 4-импульсов поля "электрич. начинки" и натяжений "упругого теста". Анализ устройства натяжений Пуанкаре выходит за рамки Э. не только из-за неизбежности квантового подхода, но даже потому, что внутри такого электрона они благодаря классич. эффектам гравитации, по-видимому, обусловливают наличие отрицат. плотности массы покоя [В. Боннор (W. Bonnor) и др., 1989].

Строго говоря, вследствие эффекта рождения электрон-позитронных пар применимость Э., по крайней мере без учёта сильных флуктуации заряда и эл.-магн. поля, проблематична уже на расстояниях меньше комптоновской длины волны электрона (П. Дирак, 1928). Вместе с тем эксперименты с электронами и мю-онами высоких энергий показывают, что при разл. взаимодействиях с др. частицами они ведут себя как точечные вплоть до расстояний ~10^-16 см.

Реакция излучения (радиационное трение). Принимая тем не менее к.-л. распределение заряда, напр. равномерное внутри шара радиуса r _е, на основе Э. можно ответить на важнейший вопрос о результате эл.-магн. воздействия разл. "частей" электрона друг на друга. Оказывается, несмотря на то, что эл.-магн. масса зависит от выбранного распределения, от него не зависит самовоздействие электрона, т. е. полная сила реакции излучения [X. Лоренц (Н. Lorentz), 1892; М. Абрагам (М. Abragam), 1904]

Она получается после перенормировки массы в первом порядке разложения по малому отношению r _е к характерному масштабу неоднородности поля (или малому параметру запаздывания e²/m_ec³t). Независимость (18) от r _е обеспечивает корректность учёта самовоздействия в пределе точечного заряда r _е 0. При этом обычно требуется условие малости силы g^a по сравнению с силой Лоренца (1') со стороны внеш. поля. Оказывается, что последнее условие достаточно выполнить в системе отсчёта, где электрон покоится и сила реакции излучения на него равна g=(gⁱ/c) =(2e²/3c³)d²u/dt². Для гармонич. полей Е, В с частотой w оно даёт ограничения (условия внутр. непротиворечивости Э.)

к-рые в a^-1 = 137 раз слабее, чем-приведённые выше квантово-электродинамич. ограничения. Второй закон Ньютона для изменения 4-импульса тсu^a точечного заряда, находящегося под действием "обычной" внешней силы (1') и "необычной" силы Лоренца-Абрагама (18), к-рая сама определяется кинематикой заряж. частицы, можно представить в более традиционной форме

если ввести понятие "эл.-магн." комплекса с эфф. 4-им-пульсом

[К. Тейтелбойм (С. Teitelboim), 1970]. Последний указывает на неразделимость заряда и его собственного ближнего поля (эл.-магн. шубы). Это "связанное" поле автоматически учитывается в локальном балансе 4-импульсов, следующем из приведённого второго закона Ньютона: приращение 4-импульса комплекса и создание 4-импульса "свободного" поля излучения происходят за счёт поглощения 4-импульса внешнего поля.

Непротиворечивое введение самовоздействия путём добавления силы (18) к силе Лоренца (I) для каждого точечного ускоренно движущегося заряда q_n в рамках Э. предполагает дополнит, условие отсутствия ускорений в областях вне поля, E=B=0. в (1). Иначе в получающихся ур-ниях движения, содержащих теперь третьи производные координат частиц r_n по времени, могли бы появиться неприемлемые решения, отвечающие неогранич. самоускорению заряда за счёт бесконечной энергии собственного поля. Разумеется, упомянутый выше "одетый" эл.-магн. комплекс вообще не испытывает самоускорения, поскольку в любой мгновенно сопутствующей системе отсчёта для перенормированного импульса справедливо ур-ние (1). Автоматич. отбор физически приемлемых решений ур-ний движения "голой" заряженной частицы, независимо от соотношения между силой реакции излучения и силой Лоренца, возможен также при их формулировке в эквивалентном интегральном виде, включающем начальные и конечные условия (Ф. Рорлих, 1961), Так, рассматривая (для простоты) нерелятивистский случай [Д. Д. Ива-ненко, А. А. Соколов, 1948; Р. Хааг (R. Haag), 1955], при конечном условии du/dt=0 (при ) имеем

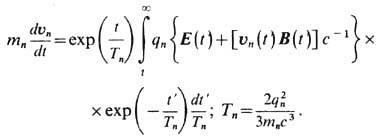
Здесь налицо формальное нарушение причинности, поскольку ускорение выражается не через прошлое, а через будущее движение частицы, т. е. определяется полями, до к-рых частица ещё не дошла, на временном интервале ~ Т _n. Однако для всех заряж. частиц (тел) времена Т _n =2r _п/3 с<= Т _е=2 е²/(3 т _е с³) 6^.10^-24 с и, следовательно, все соответствующие проблемы непричинности и нелокальности эл.-магн. взаимодействия оказываются за пределами применимости Э. А именно, принципиальным становится учёт квантовых флуктуации движения электрона (или любой заряж. частицы), для к-рых характерный временной, , и пространственный, масштабы в раз больше соответственно временного, Т _е, и пространственного, сТ _е, масштабов самоускоряющихся решений. Эти проблемы корректно разрешаются при кван-тово-электродинамич. анализе самовоздействия [Е. Мо-ниц, Д. Шарп (Е. Moniz, D. Sharp), 1977; В. К. Кривицкий, В. Н. Цытович, 1991 ]. Оказывается, что при достаточно длительном действии сила реакции излучения действительно проявляется на классич. уровне, напр., она обусловливает спиральное (скручивающееся) движение электронов в однородном магн. поле, отличающееся от винтового движения с постоянным радиусом благодаря трению о собственное синхротронное излучение.

Запаздывание. Причинности принцип играет в Э. важнейшую роль, поскольку, согласно условиям излучения (при постановке нач. задачи в ограниченной области пространства), он требует ограничиться только запаздывающими решениями ур-ний Максвелла, нарушая их обратимость во времени (при замене j -j,r r, В - В, Е-> Е Если для определённости выбрать условие калибровки Лоренца A^a_,a= 0, то вынужденное решение соответствующего (8) волнового ур-ния А^a,b_,b = 4pj^a/ с для системы точечных зарядов можно записать в виде

( Льенара - Вихерта потенциалы). Здесь интегрирование ведётся по собств. времени т„ каждой из заряж. частиц и использована запаздывающая Грина функция G(х^m )отличная от нуля только в световом конусе будущего ( х⁰>0) и равная там 2d (- х_m х^m )(для свободного пространства). Из решения (19) вытекают, по существу, все результаты Э. об излучении и взаимодействии зарядов; для пространственно ограниченных задач в нём необходимо лишь соответствующим образом изменить ф-цию Грина.

Дальнодействие. Можно совсем не вводить распределённое в пространстве поле, а подставить его явные значения в точках нахождения зарядов в ур-ния их движения. Тогда Э. примет вид теории прямого межчастичного взаимодействия с ф-цией Лагранжа, зависящей только от координат и скоростей зарядов [X. Тетроде (Н. Tetrode), 1922; А. Фок-кер (A. Fokker), 1929]. Для такой переформулировки Э. в решении (19) удобнее использовать непричинную ф-цию Грина, всюду определяемую полуразностью запаздывающего и опережающего потенциалов:

(для свободного пространства). В полевой трактовке этим учитывалось бы "свободное" поле излучения и снималась бы проблема самовоздействия и перенормировки массы в пределе точечных зарядов (П. Дирак, 1938). Вместе с тем добавлением к получающейся ф-ции Лагранжа полных производных по времени удаётся придать новой теории явно причинную форму, причём симметричную по перестановкам частиц [Р. Муре (R. Moore), Т. Скотт (Т. Scott), М. Монахан (М. Monahan), 1988]. В частности, для заряда q_k, взаимодействующего со всеми остальными зарядами Вселенной, ф-ция Лагранжа принимает вид:

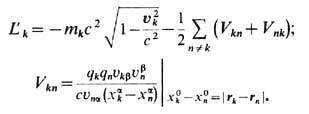
Поправка на силу реакции излучения (в нерелятивистском случае)

к запаздывающей силе Лоренца, обусловлена одними и теми же (остальными, п k )зарядами Вселенной и возникает в уравнении движения естеств. образом из требования самосогласованности движения всех заряж. частиц при условии квазинейтральности Вселенной и отсутствия элек-трич. поляризации при усреднении по всем рассматриваемым зарядам, Здесь проблема самоускорения

заряда не возникает, поскольку отсутствует внутренний бесконечный источник энергии (собственное кулоновское поле), и без силы Лоренца невозможно появление "силы реакции излучения", автоматически низведённой на роль поправки.

Что касается свойств необратимости во времени и выделения обычных запаздывающих решений, то они связываются со свойствами эволюционирующей материи и всей Вселенной и ввиду наличия неэлектромагн. сил выходят за рамки Э., требуя включения дополнит. физ. постулатов [Дж. Уилер (J. Wheeler), P. Фейнман (R. Feynman), 1945; Д. Пегг (D. Pegg), 1975]. В целом исследования Э. как теории прямого межчастичного взаимодействия направлены на то, чтобы преодолеть внутр. противоречия полевой Э., связанные с точечностью зарядов, перенормировкой их массы, нарушением причинности при самовоздействии, ограничением макс. потенциалов и мин. расстояний взаимодействия зарядов и пр. Однако, поскольку эти противоречия затрагивают лишь область квантовых явлений, применение в области классич. физики переформулированной, неполевой Э. оказывается несколько искусственным и непопулярным, особенно вследствие её усложнённости. Последнее гл. обр. обусловлено необходимостью выделения запаздывающих координат частиц, накладывающего сложные условия связи на вариац. ур-ния теории.