Особенности динамики поля с источниками

Согласно эксперим. данным, поток электрич. поля Е через S пропорционален суммарному заряду в объёме V:

Для неподвижных зарядов это утверждение следует из закона Кулона, но в Э. справедливо и при произвольном движении зарядов внутри поверхности S, несмотря на существование излучения. Тем самым устанавливается (и экспериментально подтверждается) фундам. свойство заряда Q, к-рое может служить новым способом его измерения, формально независимым от старого (1) и не апеллирующим к кинематике заряда.

Этот шаг однозначно определяет ур-ния Э. Действительно, формулировка (5) в дифференц. форме и требование её релятивистской ковариантности, т. е. выполнения при любой скорости движения инерциальной системы отсчёта с учётом преобразований координат, поля, плотностей заряда и тока, приводят к следствию

В результате магн. поле можно рассматривать как неизбежный релятивистский результат движения электрич. зарядов (тока j) и нестационарности создаваемого ими электрич. поля (тока смещения д E/дt).

Аналогичная аргументация по отношению к закону сохранения (в частности, отсутствия) магн. зарядов даёт закон эл.-магн. индукции:

С учётом ур-ний непрерывности j^a_,a= 0 и =0 независимыми оказываются только правые ур-ния в (6) и (7). (Об их записи в интегр. форме, о граничных и нач. условиях, условиях излучения и о единственности решения см. Максвелла уравнения. )Полевые ур-ния (6), (7) совместно с ур-ниями движения всех зарядов под действием силы Лоренца лежат в основе Э. В релятивистски ковариантной форме ур-ния (6) и (7) имеют вид:

Т. о., электрич. и магн. 4-плотности тока являются локальными источниками полей. Поле, порождённое движущимися зарядами, согласно (8), распространяется в свободное от них пространство независимо от источников с одной и той же скоростью с (рис. 1). Она не зависит также от выбора инерциальной системы отсчёта ввиду явной ковариантности (8). Тем самым Э. предоставляет фактич. основу для второго постулата спец. теории относительности, требующего существования инвариантной скорости распространения сигналов.

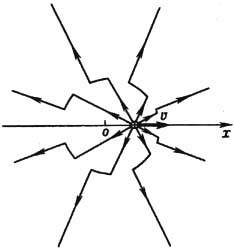
Рис. 1. Силовые линии электрического поля Е заряда q, начавшего двигаться из точки о со скоростью u.

Источники. Вместе с тем скорость u движения зарядов как источников поля в ур-ниях Максвелла формально может быть любой, в частности превышающей скорость света в вакууме [О. Хевисайд (О. Heaviside), 1889; У. Том-сон (W. Thomson), 1901; А. Зоммерфельд (A. Sommerfeld), 1904]. Последняя возможность может быть обеспечена (даже если не иметь в виду гипотетич. тахионы )совокупным движением реальных зарядов под действием разл. "зайчиков", напр. плоских импульсов фотонов, электронов или др. частиц, наклонно падающих на плоский экран, либо под действием "ножниц", где роль "зайчика" играет точка пересечения образующих "ножницы" двух лезвий. В силу неравенства u>c создаваемое "зайчиком" пятно зарядов с плотностью r может отвечать сколь угодно большой плотности тока j = ru.

В подобных и др. случаях, когда движение определённых зарядов допустимо считать заранее известным, в правых частях ур-ний (8) или (6), (7) аддитивно выделяют т. н. сторонние источники j^a _ст= (cr _ст, j _ст) и -- заданные в пространстве-времени - 4-плотности тока, для к-рых

Ограничения. Границы применимости Э. в зависимости от анализируемых реальных ситуаций и преследуемых целей могут определяться самыми различными причинами. Ниже указаны лишь наиболее типичные из них.

Важнейшим свойством ур-ний Максвелла является их линейность: поля, созданные двумя независимыми системами источников j^a_1ст, и j^a_2cт, , подчиняются суперпозиции принципу, т. е. сумма этих полей является решением ур-ний при совместном действии источников: j^a _ст=j^a_1ст+j^a_2ст, . Нарушение принципа суперпозиции полей происходит за счёт нелинейного возбуждения новых токов j^a, , индуцируемых j^a _ст, при достаточно сильных полях в среде (либо в вакууме из-за квантовых эффектов рождения и уничтожения частиц, прежде всего электрон-позитронных пар, в полях |F_ab| Е _с В _с = т² _е с³/ 4,4^.10¹³ Гс). Согласно квантовой электродинамике, вследствие рождения пар частица-античастица в достаточно сильных полях и при локализации заряж. частиц (массой т )в области с размерами порядка комптоновской длины волны /g тс возникает ограничение и на их макс. плотность тока Здесь I _А =g тс³/е- т . н. ток Аль-вена, отвечающий макс. концентрации частиц с зарядом е, движущихся прямолинейно друг за другом на расстоянии своего эл.-магн. классич. радиуса e²/gmc²= . со скоростью u~c в трубке с поперечным размером ~ ; g=1/ , a= е ²/ . Для электронов

I_A/g 17 кА.

В соответствии с неопределённостей соотношениями существуют также мин. среднеквадратичные значения полей, к-рые зависят от их частоты со и в свободном пространстве отвечают следующей спектр. плотности энергии нулевых колебаний эл.-магн. поля: [ Е²(w) + B²(w)]/8p~ (2/l)³, где l= 2p с/w. При измерении состояния полей E(ct, r), B(ct, r )как ф-ций r и t в области пространства L³ и времени Dt,aтакже при измерении их пространственно-временного среднего по этой области вследствие квантовых эффектов, обусловленных неустранимым обратным влиянием измерит. аппаратуры на поле, возникают абс. ограничения точности DE _мин = D В _мин = 2 [Л. <Д. <Ландау, Р. Пайерлс (R. Peierls), 1931] (см. также Квантовые неразрушающие измерения).

Симметрия. При локальных (точечных) преобразованиях координат и времени максимальную Ли группу симметрии, не меняющую вид ур-ний Максвелла с токами (8), составляют наряду с линейными 6-параметрич. преобразованиями Лоренца х^a x'^a =L'_b^ax^b не только очевидные 4-параметрич. преобразования сдвига х^a х'^a = х^a + а^a (см. Пуанкаре группа )и 1-параметрич. масштабные преобразования x^a х'^a = bх^a, но и нелинейные 4-параметрич. конформные преобразования (Н. Bateman, E. Cuningham, 1909)

Сопровождающие (9) конформные преобразования полей Е, В и токов j^a, . являются линейными, но явно зависят от х^a; они используются при построении нелинейных версий ур-ний Э. и нахождении их точных решений. Ур-ния Максвелла (8) не изменяются также при локальных внутренних, т. е. не затрагивающих пространственно-временные координаты, д у а л ь н ы х п р е о б р а з о в а н и я х:

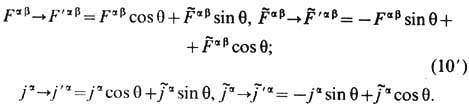
Для свободных полей они известны как 1-параметрич. п р е о б р а з о в а н и я Л а р м о р а-Р а й н и ч а

и связаны с поляризац. вырождением эл.-магн. волн. Однако преобразования (10'), как и (9), не сохраняют вид ур-ний движения (1) электрич. (или магн.) зарядов.

Магнитный заряд. Явное согласование дуальной симметрии ур-ний Максвелла и ур-ний движения имеет место только в случае дуально заряженных частиц, несущих одновременно электрич. q_n и магн. заряды. Последние преобразуются в соответствии с (10') по правилу

не изменяющему полную силу Лоренца, действующую на n -ю заряж. частицу:

Если отношение равно одной и той же (любой) величине для всех частиц, то дуальный поворот на угол приводит ур-ния Э. (8), (11) к обычной форме без магн. монополей ( =0) с наблюдаемыми эфф. электрич. зарядами частиц q'_n= и наблюдаемыми полями E', В' из (10) [Л. Пёйдж (L. Page), H. Адам (N. Adam), 1940]. Универсальность отношения для известных частиц экспериментально подтверждается с большой относит. точностью (напр., для электронов и протонов относит. погрешность не превышает ~10^-26). Это обстоятельство, позволяя исключить дуально заряженные частицы и, в частности, "чистый" магн. монополь (для к-рого отношение по величине и по знаку должно быть обратно таковому для "чистого" электрич. заряда), скрывает дуальную симметрию однозарядовой Э. Тем не менее и в ней наиб. фундаментальными естественно считать те наблюдаемые, к-рые инвариантны относительно дуальных преобразований (а не сами электрич. и магн. поля), напр. дуально симметричную силу Лоренца (11), эфф. заряд q'_n и компоненты T^mv тензора плотности энергии-импульса эл.-магн. поля (А. Зоммерфельд, 1928):

Даже в отсутствие "чистых" магн. монополей в Э. допустимы высшие магн. мультиполи, начиная с диполя, образованные магнитно нейтральной совокупностью монополей (ср. двухкварковую структуру мезонов и трёхквар-ковую структуру барионов). Однако эксперименты фактически исключают эту возможность, показывая, что все магн. мультиполи образованы электрич. токами. Так, в 1951 в экспериментах по рассеянию нейтронов в неоднородном магн. поле В= В (х) у⁰ (рис. 2) было показано

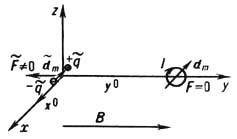
Рис. 2. Силы, действующие на "токовый" d_m и "моно польный" магнитные диполи, ориентированные против оси х° и находящиеся в неоднородном магнит ном поле В=В(х)у°.

[К. Г. Шал (С. G. Shull) и др.], что их магн. дипольный момент d_m имеет токовую [Ю. Швингер (J. Schwinger), 1937], а не монопольную [Ф. Блох (F. Bloch), 1936] природу: нейтроны движутся под действием силы F= (d_mB), характерной для рамки с электрич. током I=cd_m/pr₀². (радиуса r₀), но не силы В, характерной для двух . разноимённых монополей b = + расположенных на расстоянии l. При =d_m различие указанных сил F- .[d_mrotB]обусловлено различным взаимодействием диполей со сторонними токами j=(c/4p)rot В, создающими неоднородное магн. поле В(r).

Электромагнитная асимметрия. Т. о., вещество устроено дуально несимметрично, из одних лишь электрич. зарядов. Впрочем, по крайней мере в макроскопич. Э., это не исключает ситуации, когда в неподвижной системе проводников отлична от нуля только плотность тока (и соответствующие магн. и тороидные мультипольные моменты), тогда как плотность электрич. заряда тождественно равна нулю. Создаваемое такой системой электрич. поле Е отлично от нуля, только если токи нестационарны. При движении относительно этой системы наряду с плотностью тока в ней будут наблюдаться плотность заряда и соответствующие электрич. мультипольные моменты; однако не существует системы отсчёта, из к-рой наблюдалась бы одна только плотность заряда и не наблюдалась бы плотность тока, а следовательно, всюду отсутствовало бы магн. поле.

В общем случае, согласно (7), ввиду отсутствия магн. зарядов и независимо от движения электрич. зарядов

т. е. магн. поле выступает как вспомогательное, характеризующее историю эволюции основного электрич. поля. Несмотря на это, введение самостоят. магн. поля необходимо, если последовательно придерживаться идеи близ-кодействия зарядов, т. е. описывать их взаимодействие только посредством локально (а не интегрально) измеримых полевых величин.

Экстремальные принципы. В отличие от дуально симметричной Э. (8), (11), в однозарядовой Э. не возникает проблем с получением совместной системы ур-ний (1), (8) для движения отд. электрич. зарядов q_n и поля в вакууме из вариац. принципа (см. Вариационное исчисление). Для удобства вводятся новые полевые переменные - скалярный j( сt, r) и векторный A(ct, r) потенциалы электромагнитного поля:

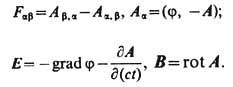(13)

Тогда второе ур-ние из (8), принимающее вид F_ab,v + F_va,b+ +F_bv,_a = 0, и, следовательно, ур-ния (7) с удовлетворяются тождественно. Первое же ур-ние из (8) и ур-ние (1') с учётом (4') [или ур-ния (6) и ур-ние (1) с учётом (4)] есть в точности Эйлера - Лагранжа уравнения с лагранжианом

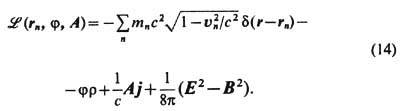
При этом, правда, в последнем слагаемом необходимо исключить бесконечную энергию собственного (кулонов-ского) поля точечных зарядов, а в слагаемом взаимодействия A_aj^a/c- самовоздействие зарядов. Поскольку наблюдаемая масса заряж. частиц т _n конечна, компенсацию их бесконечной эл.-магн. массы следует обеспечить введением бесконечной отрицат. массы неэлектромагн. происхождения ("перенормировка" массы). Эта непоследовательность, связанная с идеализацией точечных элементарных частиц, в релятивистской классич. физике, не включающей описание детальной внутр. структуры заряж. частиц, напр. как полевых образований, неизбежна в силу невозможности существования абсолютно недеформируемых протяжённых тел.

Калибровочная инвариантность. Если отказаться от то-чечности и учесть неэлектромагн. взаимодействие частиц, то, описывая частицы нек-рым классич. полем y, первое слагаемое в (14) следует заменить на более общий лагранжиан частиц , зависящий от к.-л. многокомпонентных комплексных ф-ций yk(x^a), k=1, 2, ... , и их производных y^k_,a. С учётом вещественности требование инвариантности полного лагранжиана относительно локальных фазовых преобразований

( калибровочные преобразования; обнаруживает за-мечат. факт, известный как эвристич. принцип калибровочной инвариантности и перенесённый из Э. на всю теорию поля [Ч. Янг (Ch. Yang), P. Миллс (R. Mills), 1953; M. Гелл-Ман (М. Gell-Mann), 1956]. Согласно этому принципу, инвариантность исходного лагранжиана восстанавливается удлинением производных

за счёт введения компенсирующего поля A_a( х^b), преобразующегося одновременно с (15) по т. н. калибровочному закону

не меняющему наблюдаемые компоненты поля (13) F_ab. [В (15') величина заряда электрона е выступает как константа введённого таким образом взаимодействия - мин. эл.-магн. взаимодействия,- давая ещё одно неявное определение электрич. заряда.] Если для определённости ограничиться линейной зависимостью от производных y^k_,a, характерной для спинорных полей вещества, то в полном лагранжиане

непосредственно возникает необходимый лагранжиан взаимодействия вместе с новым определением 4-плотности тока , не связанным с точечностью зарядов [ср. (4), (14)].

Собственный лагранжиан компенсирующего (здесь - эл.-магнитного) поля выбирается в простейшем виде [см. (3), (13)], обеспечивающем его инвариантность при калибровочном преобразовании (15 ") в отсутствие вещества. Этим, в частности, исключается слагаемое вида а следовательно, возможность ненулевой массы фотона Наличие ненулевой массы фотона кардинально меняло бы законы Э. на расстояниях [Л. де Бройль (L. de Broglie), 1924]; однако земные эксперименты, в частности по проверке закона Кулона и независимости скорости эл.-магн. волн в вакууме от их частоты, допускают такую возможность только на расстояниях 10¹⁰ см, а наблюдения стабильных конфигураций газа и магн. полей галактик - на расстояниях 10²² см. В принципе было бы возможно также несохранение электрич. заряда, напр. распад электрона на нейтральные частицы или осцилляции электрон <-> позитрон, хотя подобные процессы и подавлены неизбежным участием большого кол-ва ( 10¹³ -10²¹) сверхмягких продольных фотонов (Я. Б. Зельдович, Л. Б. Окунь, М. Б. Волошин, 1978); однако лабораторные эксперименты и глобальные геоэлектрич. оценки показывают, что время жизни электрич. заряда превышает 10³⁰ с.