33. Асимптоты графика функции. Пример.

Асимптотой графика функции f(x) называется прямая, расстояние до которой от точки графика (х y=f(x) ) → 0 при стремлении этой точки по кривой бесконечности.

Прямая х=а называется вертикальной асимптотой графика, если хотя бы один из односторонних пределов при х →а+-0, = + ∞ или -∞.

Если функция f(x) определена и непрерывна для любых х>M (х<M), то говорят, что прямая y=kx+b, является правой (левой) асимптотой кривой y=fx, если при х→+∞ или ч→-∞.

f(x)= kx+b+α(x), где α(х) – бесконечно малая.

Для того, чтобы график функции у=f(x) имел при х→+∞ (х→-∞) асимптоту, необходимо и достаточно, чтобы существовали начальные пределы.

(F(x)-kx)=b

И тогда прямая у=Кх+б является правой (левой) асимптотой.

Замечание!

Если К=0, то у=б.

Если К=∞ или б=∞ то асимптоты нет.

У однозначной функции может быть только одна правая или только одна левая асимптота.

34. Схема графика построения функции.

1. Найти область определения функции промежутка непрерывности.

2. Исследовать четность-нечетность, периодичность.

3. Найти нули функции, области построения знака.

4. Найти точки разрыва, классифицировать их.

5. Найти асимптоты графика.

6. Исследовать функцию на экстремумы. Найти интервалы возрастания и убывания.

7.Найти точки перегиба направления выпуклости и вогнутости.

8. Построить график.

35. Неопределенный интеграл и его свойства.

Определение первообразной и неопределенного интеграла

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как

Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная. 

Свойства неопределенного интеграла

В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,  а, k, C - постоянные величины.

36. Метод непосредственного интегрирования. Подстановки. Примеры.

Метод подстановки (замены переменной)

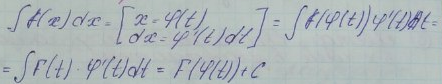
Пусть функции y=f(x) x=ᶲ(фи)(t) определены на числовых промежутках ∆х и ∆t, причем ᶲ(фи)( ∆t) входит в числовой промежуток ∆х.

Функция ᶲ(фи)( t) непрерывна на множестве ∆t и дифференцируема во внутренних точках этого промежутка, тогда, если функция f(x) имеет первообразную F(x) на множестве ∆х, то и функция f(ᶲ(фи)( t))* ᶲ(фи)’( t) имеет первообразную на множестве ∆t равную F(ᶲ(фи)( t))

37. Метод интегрирования по частям. Пример.

Если функции u(x), v(x) непрерывны на некотором числом промежутке и дифференцируемы в некоторых точках этого числового промежутка, и если существует интеграл v(x)du на этом числовом промежутке, то тогда существует и интеграл u(x)du , причем

Формула интегрирования по частям:

38. Интегрирование рациональных дробей (многочлены с действительными корнями).

39. Интегрирование рациональных дробей (многочлены, не имеющие действительных корней)

40. Интегрирование иррациональностей.

Для интегрирования иррациональной функции, содержащей   используется подстановка  .  Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме  , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.  Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида  , интегрируется с помощью подстановки  . 

Пример:

Найти интеграл  .

Решение.

Сделаем подстановку:

      

Вычислим интеграл