15. Классификация точек разрыва. Примеры.

Точки разрыва

Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .

Устранимые точки разрыва

Если предел функции существует, но он не совпадает со значением функции в данной точке:

тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).

Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.

Точки разрыва первого и второго рода

Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:

• если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

• если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

31. Восстание и убывание функций. Пример.

Для того, чтобы дифференцируемая функция на интервале (а,б) возрастала (убывала) на это интервале необходимо и достаточно, чтобы во всех точках этого интервала производная была не отрицательная: F’(x)>=0 (не положительная: F’(x)<=0)

Замечание!

Если на интервале (а,б) F’(x)>0, то функция строго возрастает, если F’(x)<0, то строго убывает.

Пусть функция y=f(x) определена в некоторой окрестности точки Xо. Точка Хо называется точкой максимума (минимума), если для любых Х из этой окрестности:

f(x)<=F(Xo), f(x)>=F(Xo)

Замечание!

Если f(x)<F(Xo), то точка Хо – точка строгого максимума.

Точки максимума и минимума называются точки экстремума.

32. Выпуклость графика функции. Точки перегиба. Пример.

Кривая y=f(x) обращена в точке Хо выпуклостью к верху (к низу), если существует такая окрестность в точке Хо, что для любого х в этой окрестности касательная к кривой в точке Хо расположена выше самой кривой.

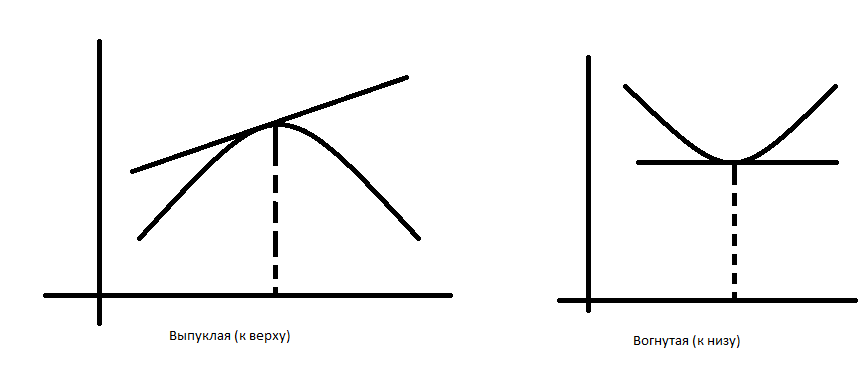
Точка Хо называется точкой перегиба, если при переходе через Хо кривая меняет направление выпуклости.

Необходимое условие существования точки перегиба:

Если Хо точка перегиба кривой y=f(x) и в этой точке существует вторая производная, то она обязательно равна 0. f”>(Xo). (В противном случае производной в этой точке не существует)

Достаточные условия существования точки перегиба:

Если функция y=f(x) дифференцируема в точке Хо, дважды дифференцируема в некоторой окрестности точки Хо, и 2 производная меняет знак при переходе аргумента через точку Хо, то Хо является точкой перегиба.

Кривая y=f(x) называется выпуклой вверх (вниз) на отрезке (а,б), если любая дуга в этой кривой в точках Х1 и Х2 расположена не ниже (не выше) её хорды.

Пусть функция y=f(x) непрерывна на отрезке [a,b] и имеет вторую производную на интервале (а,б), для того, чтобы кривая F(x) была выпуклой кверху (книзу) необходимо и достаточно, чтобы для любого х из интервала (а,б) выполнялось неравенство f”(x)<0, f”(x)>0.

Пример: