46.Интегрирование по частям в определенном интеграле. Пример.
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа о свойствах определённого интеграла, получим
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
получаем формулу интегрирования по частям для вычисления определенного интеграла:
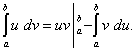(1)
Разобраться
Пример
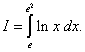
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (1) находим
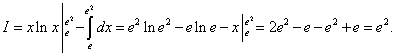
47.Геометрические приложения определенного интеграла.(площади) пример.
1. Вычисление площади плоской фигуры
1.1.
Пусть функция f(x)
непрерывна и неотрицательна на отрезке
[a,
b].
Тогда
площадь фигуры, ограниченной осью ОХ,
отрезками прямых x
= a,
x
= b
и графиком функции y=f(x),
может быть вычислена по формуле
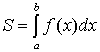(см. 10.1 рис. 1).
1.2.
Если f2(x)>f1(x)
на отрезке [a,
b],
f1(x),f2(x)
непрерывные функции, то площадь фигуры,
ограниченной прямыми х
= а,
x
= b,
графиками функций
вычисляется по формуле
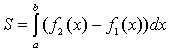(рис. 10).
1.3.
Если функция
на отрезке [a,
b]
принимает значения разных знаков,
то площадь фигуры, заключенная между
кривой y=f(x)
и осью OX,
равна
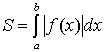(рис. 11).
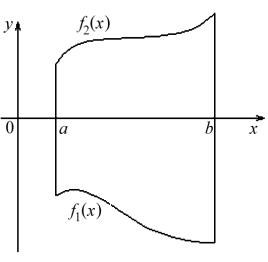
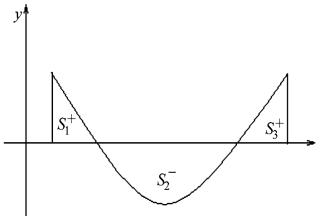
рис. 10 рис. 11
П
р и м е р 15. Вычислить площадь фигуры,
ограниченной графиками функций
и
.
Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему
=
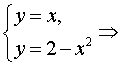
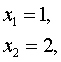
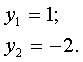
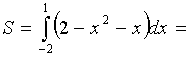
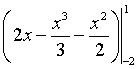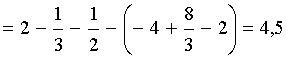кв. ед. (рис. 12).
1.4.
При вычислении площади криволинейной
трапеции, в случае когда
верхняя
граница задана параметрическими
уравнениями
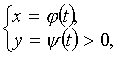
t
в формуле
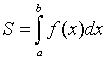надо сделать замену переменной, положив
,
тогда получим
,
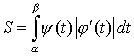где
и
з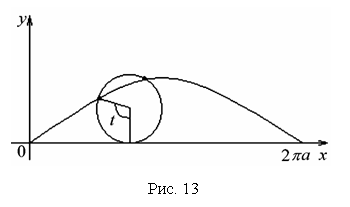
начения
параметра t,
соответствующие значениям x=a
и x=b,
т.
е.
.
П
р и м е р 16. Найти пло-щадь фигуры,
ограниченной одной
аркой циклоиды
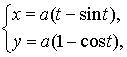
и осью
.
Замечание. Циклоида плоская кривая, которую описывает точка М окружности радиуса a, катящаяся без скольжения по прямой линии (рис. 13)
Решение. Искомая площадь
;
.
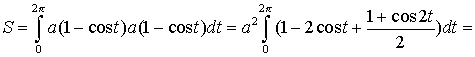
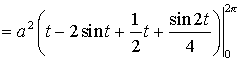
П
р и м е р 17. Вычислить площадь фигуры,
ограниченной линиями, заданными
уравнениями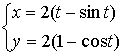
,
y
= 2
.
Решение. Из условия задачи следует, что y>0 при любом t. Решим неравенство
,
,
.
Но
по условию
.
При k
= 0
2
t
3
2
,
.
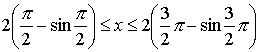При
x
не будет принадлежать интервалу
.
Фактически нужно вычислить площадь
фигуры, заключенной между прямой y
= 2
и частью циклоиды, расположенной выше
этой прямой (рис. 14).
Искомая площадь
.
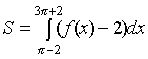
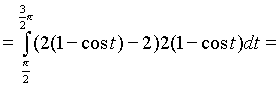
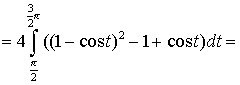
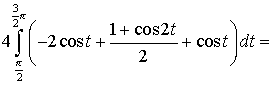
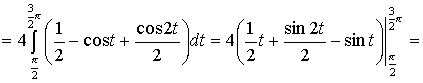
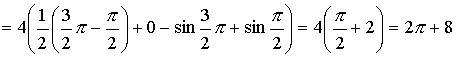2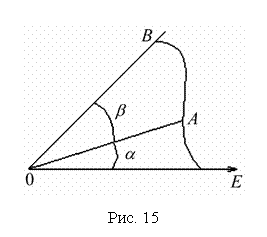
.
Вычисление площади криволинейного
сектора. Пусть
кривая AB
зада-на в полярных координатах уравнением
,
,
причем
непрерывная и неотрицательная на отрезке
функция. Фигуру, ограниченную кривой
AB
и двумя полярными радиусами, составляющими
с полярной осью углы
,
будем называть криволинейным
сектором.
Площадь криволинейного сектора может быть вычислена по формуле
.
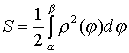(27)
П
р и м е р 18. Вычислить площадь фигуры,
ограниченной кривой
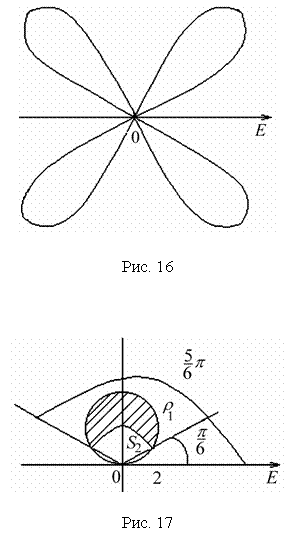
(4-лепестковая роза
рис. 16).
Решение.
Меняя непрерывно
от
0
до
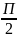, можно построить первый лепесток.
Составим таблицу значений функций
(табл. 3).
|
0 |
|
|
|
|
|
|
|
0 |
2 |
|
4 |
|
2 |
0 |
Вычислим площадь одного лепестка по формуле (27)
.
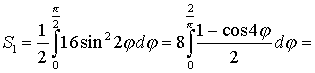
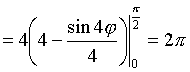Следовательно, площадь всех лепестков S=8П.