43. Свойства определенного интеграла. Примеры.
1.
2.если ф-ция f(x) интегрируема на отрезке [a b] то она интегрируема на любом отрезке содержащ-ся в [a b]
3.пусть
сущ-ет внутренняя точка с отрезка [a
b] если сущ-ют
то справедливо равенство
=
+
4.если ф-ция f(x) и g(x) интегрируемы на отрезке ab то справедливо равенство
5.const
можно выносить за знак
при
условии, что функция
интегрируемы
6.если
ф-ции f(x) и
g(x) интегрируемы
на отрезке ab то их
произведение так же интегрируемо
(
произведения
не равен произведению
)
7.если ф-ция f(x) ≥0 не отрицательна и интегрируема на отрезке ab то интеграл от нее так же не отрицателен.
8.
9.
10.если f(x) интегрируема на отрезке ab то и модуль │f(x)│интегрир. На отрезке ab.
Причем
│
│≤
44. Формула Ньютона-Лейбница и ее применение. Пример.
Теорема: Если F(x) есть какая-либо первообразная от непрерывной функции f(x) то справедлива формула.
(Пусть на некотором отрезке [a;b] оси Ох задана некоторая непрерывная функция f. Положим, что эта функция не меняет своего знака на всем отрезке
Если f есть непрерывная и неотрицательная на некотором отрезке [a;b] функция, а F есть её некоторая первообразная на этом отрезке, тогда площадь криволинейной трапеции S равна приращению первообразной на данном отрезке [a;b].)
Пример.
Вычислить
интеграл
.
Решение.
Применяя формулу Ньютона-Лейбница, получаем
45.Замена переменной в определенном интеграле.
Теорема 1. Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.
В таком случае
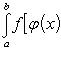
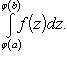(22)
Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.
Переходя к доказательству теоремы, обозначим интегралы, входящие в левую и правую части формулы (22), соответственно через Iлев и Iправ.
Пусть F(z) - функция первообразная для f(z). Тогда по формуле Ньютона-Лейбница
Iправ = F[φ(b)] - F[φ(a)]. (23)
Что же касается Iлев, то
Но согласно теореме будет
Значит,
Iлев = F[φ(b)] - F[φ(a)].
Отсюда и из (23) следует, что Iлев = Iправ.
Пример 1.
Здесь применена подстановка ln x = z (причем формула (22) прочитывалась слева направо).
Пример 2.
Здесь применена подстановка x = R sin t, и формула (22) прочитывается справа налево. Дальнейшее вычисление просто:
и окончательно
Теорема 2. Если u(x) и v(x) - две функции, заданные на промежутке [a, b] и имеющие там непрерывные производные, то
(24)