2.2. Аэродинамические трубы кратковременного действия

Основной недостаток аэродинамических труб непрерывного действия заключается в том, что мощности, необ­ходимые для их работы, очень велики, особенно при сверхзвуковых скоростях потоков газа. Поэтому при исследовании сверхзвуковых потоков используются трубы кратковременного действия. Размеры рабочей части современных труб превосходят 1 м, а числа М, получае­мые в них, достигают значений, равных 27. Для измерения давлений и скоростей газа в таких трубах требуется быстродей­ствующая аппаратура.

Конструкции труб можно разделить на два типа: схема с истечением из баллонов сжатого воздуха и схема с истечением в вакуумную емкость (рис. 2.3).

По первой схеме (рис. 2.3, а) труба состоит из компрессора 1, устройства для осушки воздуха 2, емкости для сжатого воздуха 3, быстродействующего крана 4, подогрева­теля 5 и рабочего участка трубы, состоящего из коллектора 6, сопла 7, рабочей части 8 и диффузора 9. Выбрасывание воздуха в атмосферу и глушение шума производится с помощью выхлоп­ной шахты 10.

В вакуумной установке (рис. 2.3, б) воздух из атмосферы, пройдя осушитель 1, попадает в рабочий участок, состоящий из коллектора 2, сопла 3, рабочей части 4 и диффу­зора 5. Впуск воздуха производится быстродействующим краном 6. Разрежение в вакуумной емкости 7 создается насосом 8. В качестве вакуумных емкостей используются стальные шары диаметром до 20 м.

Сопла и диффузоры сверхзвуковых аэродинамических труб могут иметь регулируемые горла. Быстродействующие краны должны открываться в течение долей секунды.

2.3. Ударные трубы

Для изучения движений при больших числах М используются ударные трубы. Ударная труба пред­ставляет собой трубу прямоугольного сечения, разделенную перегородкой (диафрагмой) на две неравные части: меньшую – камеру высокого давления и большую – ка­меру низкого давления. Площадь поперечного сечения труб меняется от нескольких квадратных сантиметров до квадратного метра и более. Длина труб достигает десяти метров. Разделяющая трубу диафрагма изго­товляется обычно из фольги, тонких металлических пластин и т.п.

Для работы трубы в камеру высокого давления подают газ под большим давлением или в ней резко повышают давление путем взрыва горючей смеси или мощного электрического разряда. Диафрагма разрывается, и по трубе низкого давления распространяется волна сжатия (ударная волна). Ударная волна, бегущая по частицам невозмущенного газа в камере низ­кого давления, создает за собой спутный поток газа, имеющий вполне определенную скорость (меньшую, чем скорость самой волны). Ударная волна движется быстро и имеет малую толщину. Спутный поток движется достаточно долго, и в нем можно произвести измерения.

Интенсивность ударной волны определяется отношением дав­лений в камерах высокого и низкого давления; температура в спутном потоке ударной волны может достигать высоких значений (до 30 000 К).

В ударных трубах можно создавать волны с чис­лами М > 50.

2.4. Приборы для измерения скоростей в потоках газа

Наиболее широко распространены при испытаниях систем и агрегатов двигателей внутреннего сгорания и турбин методы измерения скоростей специальными трубками, цилиндрическими и шаровыми зондами. Устройство этих пневматических приборов основано на использовании уравнения Бернулли. Если в некоторой точке потока необходимо знать значение скорости, то в эту точку устанавливают продольно обтекаемую трубку (рис. 2.4).

С

С₁

С₁

Р₁

Ψ₀

Р₂, С₁

Ψ₀

А

1

1

0

0

2

2

Рис. 2.4. Изменение скорости в потоке газа

с помощью измерительной трубки

В соответствии с уравнением закона сохранения энергии поток обладает кинетической и потенциальной энергией, сумма которых остается постоянной для каждой линии тока. Линия тока Ψ₀–Ψ₀ в точке А образует критическую точку, в которой скорость потока (кинетическая энергия) обращается в нуль, так как точка А неподвижна. Это вызывает соответствующее увеличение давления, которое может быть измерено с помощью дифференциального манометра (для точки А кинетическая энергия потока превращается в энергию давления). По увеличению давления можно рассчитать скорость набегающего потока. Трубка для измерения скорости должна быть малого диаметра по сравнению с диаметром рабочей части аэродинамической трубы (не вносить искажений в набегающий поток).

Уравнение Бернулли (закона сохранения энергии) для сечений 1 – 1 и 0 – 0 нулевой линии тока будет иметь вид

с₁²/2 + P₁ = с₀²/2 + Р₀,

где с₁, с₀ – скорости потока в соответствующих сечениях;

ρ – плотность газа;

Р₁, Р₀ – давление в соответствующем сечении.

Так как с₀ = 0, то значение скорости с₁ равно

.

Полное давление Р₀ может быть определено, если в критической точке сделать отверстие и тонкой трубкой соединить его с дифференциальным манометром. Давление Р₁ определяют с помощью отверстия, размещенного в сечении 2 – 2, в котором скорость равна с₁. Отверстие в сечении 2 – 2 называется статическим, так как позволяет определять статическое давление в потоке. Разность давлений Р₀ – Р₁ измеряют дифференциальным микроманометром в миллиметрах водяного столба. Впервые трубки для измерения скорости потока были предложены французским ученым Пито в 1732 г., поэтому такие трубки называют трубками Пито.

Приведенная формула для определения скорости потока используется при измерениях дозвуковых скоростей.

Рассмотрим пример определения скорости потока с помощью трубки Пито.

Пример. Дифференциальный манометр, подключенный к трубке Пито, показывает перепад давления Р = 70 мм вод. ст. Температура окружающего воздуха Т = 293 К; атмосферное давление Р₁ = =740 мм рт. ст. Определить скорость потока газа с₁.

Решение. Универсальная газовая постоянная R = 287,14 Дж/(кгК).

Р = 70 мм вод. ст. = 700 Па, так как 1 мм вод. ст. = 10 Па.

Следовательно, Р₁ = (740/760) 10⁵ = 0,974 10⁵ Па.

Согласно уравнению Менделеева – Клапейрона , т.е.

Тогда скорость потока

= 34,8 м/c = 125,3 км/ч.

Из приведенного примера видно, как легко измеряется скорость потока с помощью трубки Пито.

Для определения направления скорости в плоском потоке применяются различные насадки. Их широкое применение объясняется не только высокой точностью определения направления скорости, но и возможностью одновременно измерять значения давления скорости и полного напора. Наиболее часто применяются цилиндрические, рожковые и хоботковые насадки, рис. 2.5.

Первый из них представляет собой цилиндрическую трубку с тремя отверстиями, расположенными в плоскости, перпендикулярной к образующей цилиндра. Два боковых отверстия расположены симметрично относительно центрального. У рожковых и хоботковых насадков отверстия расположены на концах трех тонких трубок. В хоботковом насадке трубки расположены так, что их приемные отверстия находятся близко друг от друга. Недостаток рожковых и хоботковых насадков – значительное перемещение их приемных отверстий при повороте насадка вокруг оси державки. Для устранения этого недостатка державку насадка изгибают так, чтобы при ее вращении приемные отверстия находились на оси вращения. Насадки работают в плоском потоке. Державку насадка поворачивают до тех пор, пока давления в двух боковых отверстиях не сравняются друг с другом. Тогда центральное отверстие, соединенное с трубкой Пито, окажется расположенным точно против н аправления потока, и трубка Пито, находящаяся в центральном отверстии и соединенная с дифференциальным микроманометром, позволит определить значения скорости потока. Если же в насадке центральное отверстие отсутствует, а имеются только два боковых, то такой насадок называется угломерным и измеряет только направление потока (рис. 2.6).

Для определения значения и направления скорости потока в пространственном потоке применяют шаровые зонды.

Шаровой зонд представляет собой шарик с пятью отверстиями, просверленными в двух перпендикулярных друг к другу диаметральных плоскостях (рис. 2.7).

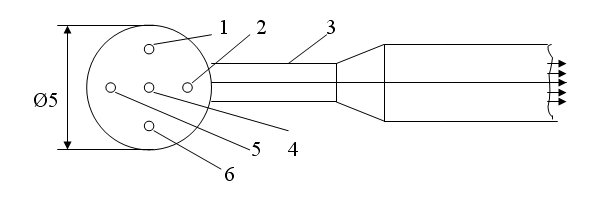
Рис. 2.7. Конструкция шарового зонда

Шарик имеет диаметр около 5 мм и помещен на цилиндрической державке 3. Угол между осями центрального и каждого из боковых отверстий шарика составляет 40^°. Каждое отверстие, как и в насадках, соединяется тонкими трубками, проходящими внутри державки, со штуцерами, имеющимися на противоположном конце зонда. Через эти штуцеры отверстия зонда соединяются с дифференциальными манометрами. Вращая шарик с помощью державки вокруг ее оси, при любом направлении потока можно получить такое положение шарика, при котором давления в точках 2 и 5 одинаковы. Очевидно, что при этом вектор скорости потока будет лежать в плоскости, проходящей через отверстия 2, 4 и 5, и задача измерения скорости выполняется, как и для насадка. Для пространственных потоков давления в отверстиях 1, 6 и 2, 5 должны быть попарно одинаковы, но при этом не обязательно давления в отверстиях 1, 6 и 2, 5 должны совпадать по значению. Для обеспечения попарного равенства давлений шарик с помощью державки поворачивается последовательно вокруг двух осей. Тогда отверстие 4 оказывается расположенным на оси пространственного потока, показывает его направление, и с помощью установленной в нем трубки Пито определяется скорость потока жидкости или газа.

Трубка Пито имеет высокое быстродействие, малые размеры (диаметр менее 1 мм) и применяется для измерений в узких т руднодоступных каналах, например в межлопаточных каналах турбины. При измерениях в медленно меняющихся потоках (в гидравлических трубопроводах) используют другие приборы – расходомеры Вентури (рис. 2.8). Принцип работы такого измерителя скорости также основан на законе сохранения энергии. Если в трубопроводе течет жидкость, то два пьезометра, установленных в различных сечениях потока, покажут различное давление. В сечении с меньшим сечением скорость потока будет выше, а давление ниже, чем в сечении большей площади. Дифференциальный манометр, подключенный к отверстиям в различных сечениях, покажет перепад давления ΔР. Зная диаметры сечений, в которых производится измерение, можно определить скорость и расход жидкости.

Рассмотрим последовательность определения скорости на примере.

Пример. Несжимаемая жидкость плотностью ρ течет по горизонтальной круглой трубе переменной площади поперечного сечения. Разность давлений Р₁ – Р₂ жидкости между площадями F₁ и F₂ измеряется с помощью дифференциального манометра. Определить массовый расход жидкости.

Площадь сечения круглой трубы равна

Уравнение Бернулли для двух сечений записывается в виде

Это уравнение должно быть дополнено уравнением неразрывности потока

Из этого выражения следует

Подставим полученное выражение для скорости в уравнение закона сохранения энергии (уравнение Бернулли) и после простых преобразований получим

где

Расход жидкости Q может быть определен по зависимости

Таким образом, скорость и расход газа (жидкости) в трубопроводе может быть определен с помощью установки в трубопровод «мерной шайбы», представляющей собой местное сужение потока, причем диаметр отверстия мерной шайбы (меньший, чем диаметр трубопровода) должен быть известен.