Контрольные вопросы

1. Какое движение газа называется одномерным?

2. Как записывается уравнение неразрывности потока в дифференциальном виде?

3. Как применяется уравнения Бернулли для сжимаемой жидкости?

4. Какая скорость потока называется максимальной? От чего зависит максимальная скорость потока?

5. Какая скорость потока называется критической?

6. Какие существуют виды воздействий на поток газа?

7. Как влияет сужение потока на его скорость, если поток имеет сверхзвуковую скорость?

8. Как устроено геометрическое сопло?

9. Как работает тепловое сопло?

10. Почему одно и то же воздействие на дозвуковой и сверхзвуковой поток приводит к противоположному результату?

11. Как влияет трение на движение газа в трубе?

12. Может ли быть достигнута скорость звука в трубе постоянного сечения, если на поток действует только сила трения?

13. Какие параметры потока называются критическими?

14. Как в расчетах потоков газа используются безразмерные скорости?

Глава 5. Плоские дозвуковые и сверхзвуковые течения газа

При исследовании течения газа в каналах, в том числе в межлопаточных каналах турбин, поток газа часто можно рассматривать как плоский. Параметры плоского течения газа зависят от двух координат – x и y.

5.1. Потенциальное движение газа. Потенциал скорости

Безвихревое течение газа при отсутствии сил трения называется потенциальным. В потенциальном течении отсутствуют вихри (отсутствует вращательное движение жидкой частицы), т.е.

ω_х = ω_у = ω_z = 0.

Отсутствие вращательного движения жидкой частицы математически означает, что существует некоторая функция координат Ф(x,y,z), частные производные от которой по координатам равны проекциям скорости на соответствующие оси координат, т.е.

.

Функция Ф(х,у,z) называется потенциалом скорости. Понятие потенциала скорости в механике жидкости и газа тождественно понятию потенциала сил в механике твердого тела: производная потенциала сил по какому-либо направ­лению дает проекцию потенциальной силы, действующей в этом направлении.

Потенциальное движение га­за в изолированной системе является изоэнтропийным, т.е. если поток газа безвихревой и силы трения малы, то тече­ние газа описывается некоторой функцией координат Ф(x,у,z).

Уравнение потенциала скоростей записывается для плоского установив­шегося потока с помощью уравнений Эйлера

(5.1)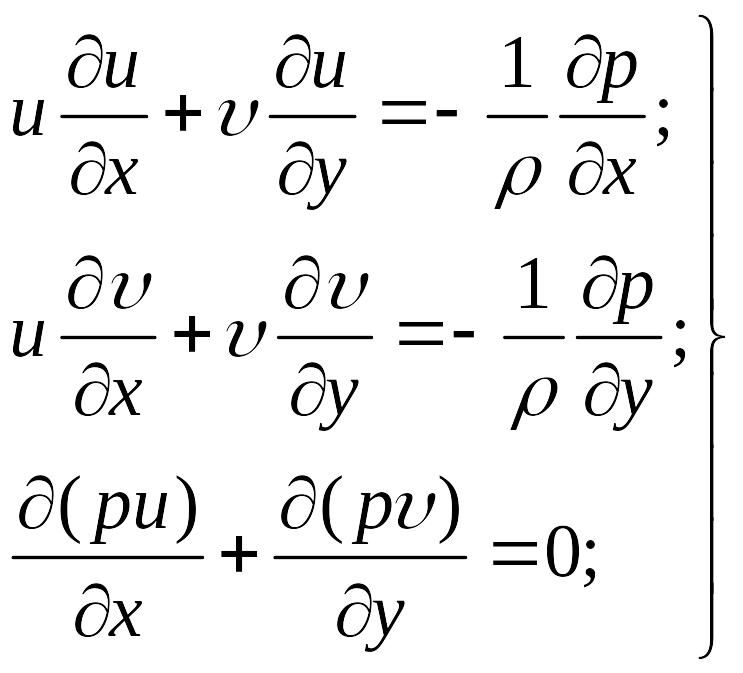

в виде

(5.2)

Уравнение (5.2) является нелинейным дифференциаль­ным уравнением потенциала скоростей в частных производных второго порядка. Введение потенциала скорости позво­лило систему трех уравнений (5.1) свести к одному и умень­шить число неизвестных, так как Ф является единственной неизве­стной функцией. Если в исследуемом поле потока известен потенциал скорости Ф(х,у), то при заданных граничных условиях могут быть однозначно определены все па­раметры течения.

Таким образом, при исследовании плоских потенциальных движений га­за необходимо определить потенциал скоростей Ф(х,у) для данного вида движения, т.е. решить уравнение (5.2).

Уравнение (5.2), по которому оп­ределяется потенциальная функция Ф(х,у), показывает, что оно приобретает различную форму в зависимости от соотношения ме­жду составляющими скорости u, v и скоростью звука а. Если величины u/а и v/a малы, т.е. если скорость потока газа мала по сравнению со скоростью звука, то поток является несжимаемым. Для несжимаемого потока Ф = Ф_н и

(5.3)

Уравнение Лапласа (5.3) характеризует потенциальное течение идеальной несжимаемой жидкости. При больших дозвуковых ско­ростях, когда влиянием сжимаемости пренебречь нельзя, нелиней­ное дифференциальное уравнение (5.2) значительно упрощается, если поток можно считать слабо возмущенным.