3.5. Уравнение сохранения энергии вязкого теплопроводного газа

Уравнение закона сохранения энергии для идеального сжимаемого газа (3.11) не учитывает влияние вязкости и теплопроводности газа.

Получим уравнение закона сохранения энергии для выделенного элемента жидкости (рис. 3.2) с учетом вязкости жидкости. Изменение его кинетической и внутренней энергии равно сумме работ внешних и внутренних сил и подведенного количества теплоты. Работа внутренних сил давления, приложенных к левой и правой граням за единицу времени, определяется по соотношению

Касательные силы на этих гранях производят работу

и .

Работа внутренних сил давления и трения по всей поверхности элемента выражается соотношениями

Работа внешних сил выражается соотношением

.

Обозначим Q – количество теплоты, передаваемой частице газа за единицу времени (отнесенное к ее массе ρdxdydz), – удельное количество теплоты, передаваемое единице поверхности частицы за единицу времени. В соответствии с законом Фурье q = – λ gradT (λ – коэффициент теплопроводности).

Запишем без вывода уравнение закона сохранения энергии вязкого теплопроводного газа в векторной форме

Здесь – вектор сил внешних полей; – векторы внутренних сил; i^* – полная удельная энтальпия заторможенного потока.

Уравнение закона сохранения энергии вязкого теплопроводного газа может быть записано и иначе:

(3.12)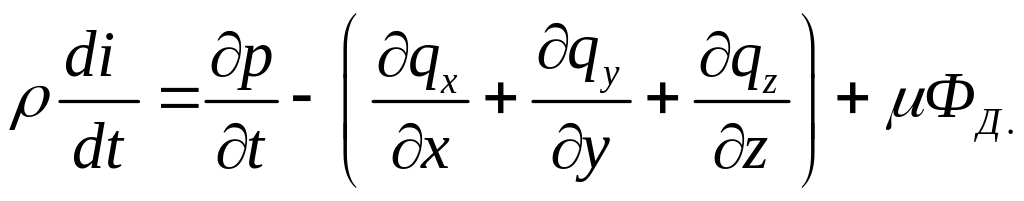

Здесь

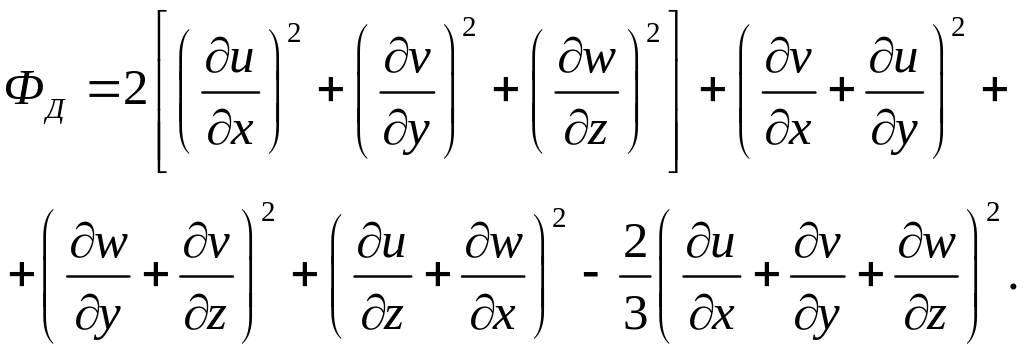
Ф_Д – диссипативная функция, пропорциональная работе внутренних сил трения, а q_x, q_y и q_z – тепловые потоки в направлении координатных осей х, у, z.

В уравнение (3.12), кроме коэффициента вязкости μ, входит коэффициент теплопроводности газа λ, зависящий от температуры. С повышением температуры коэффициент теплопроводности λ увеличивается в связи с интенсификацией переноса теплоты. Значение коэффициента теплопроводности λ может быть определена по формуле Сатерленда

где λ₀, T₀ – коэффициент теплопроводности и температура, соответствующие начальному состоянию газа; T_s = 114К – постоянная Сатерленда для воздуха.

3.6. Вихревое движение

Вихревое движение – это вращение элементарного объёма вокруг некоторой оси, проходящей через этот объем. Такое движение называется вихрем и характеризуется угловой скоростью ω. Вихрь – величина векторная, вектор вихря направлен перпендикулярно плоскости вращения. Угловая скорость вращения частицы ω раскладывается на составляющие ω_x, ω_y, ω_z, параллельные соответствующей оси координат, причем

.

Вихревой линией называют такую линию в потоке, в каждой точке которой на­правление вектора угловой скорости совпадает с направлением касатель­ной к этой линии. Урав­нение вихревой линии

Поверхность, образованная вихревыми линиями, проведенными через точки бесконечно малого замк­нутого контура, называется вихревой трубкой. Частицы, находящиеся во вращательном движении и заполняющие вихревую трубку конечного размера, образуют вихревой шнур. Вихревая трубка бесконечно малого сечения называется вихревой нитью. Если вращение жидкости про­исходит с постоянной скоростью и положение вихря с течением времени не изменяется, вихревое движение является стационарным.

Вихри образуются в тех случаях, когда смешиваются два или более потоков жидкости или газа, движущиеся с различной скоростью. Так, при обтекании спинки крыла скорость потока газа больше, чем в корытце, поэтому на задней кромке крыла встречаются два потока с различной скоростью, что вызывает появление вихря. Вихри образуются в пограничном слое, при внезапном расширении потока, при обтекании тел потоком газа и др.

Вихрем называется вектор, равный удвоенному значению вектору мгновенной угловой скорости ω; вихрь обозначается Ω.

Скалярное произведение вихря на вектор площадки (т.е. поток вектора через площадку ) называется напряженностью вихря I

где σ_x, σ_y, σ_z – проекции площадки на оси координат, причем проекция σ_x расположена перпендикулярно плоскости YOZ.

Вторая теорема Гельмгольца. Напряженность вихря I на всей его протяженности остается постоянной

Т ак как напряженность вихря остается постоянной, то уменьшение площади сечения вихря приводит к увеличению угловой скорости вращения частиц. При радиусе вращения, равном нулю, угловая скорость вращения вихря должна стать бесконечно большой , что физически невозможно. Поэтому вихри не могут появляться или исчезать внутри жидкости или газа. Вихри либо опираются на какую-либо поверхность, либо замыкаются сами на себя, образуя вихревое кольцо, рис. 3.3.

Определение интенсивности вихря экспериментальным путем связано с непреодолимыми трудностями. Поэтому интенсивность вихря определяется через циркуляцию скорости.

Теорема Стокса. Интенсивность вихря равна циркуляции скорости по замкнутому контуру, один раз опоясывающему вихревую трубку.

Ц иркуляции ско­рости определяется по уравнению

где – проекция вектора скорости на направление элемента контура l. При вычислении циркуляции положительным направлением обхода считают такое направление, при котором заключенная внутри контура область по­тока остается справа. Циркуляция имеет физический смысл работы вектора скорости (произведение скорости на путь).

Теорема Томсона. Если массовые силы имеют однозначный потенциал и движение идеальной жидкости баротропно, то циркуляция скорости по замкнутому контуру будет постоянна.

Движение жидкости является баротропным, если её плотность является функцией одного давления. Это наблюдается в изотермическом и адиабатическом процессах.

Из этого утверждения следуют два вывода:

1. Если в баротропной жидкости в некоторый момент времени циркуляция по замкнутому контуру равнялась нулю, то она останется равной нулю и в последующие моменты времени, т.е., если движение было безвихревым, то оно останется безвихревым.

2. Интенсивность вихревой трубки идеальной жидкости не изменяется с течением времени.

Следовательно, в идеальной жидкости вихри не могут возникать. В реальной жидкости из-за вязкости вихри возникают и исчезают. Однако если в начальный момент времени вихрей в жидкости не было, то они могут появляться только попарно, причем равными по значению, но противоположными по направлению.