
Цифровая обработка сигналов
Digital signal processing
Тема 0: оконное преобразование фурье
Ни одна вещь не возникает и не уничтожается, но каждая составляется из смешения существующих вещей или выделяется из них.
Анаксагор. Древнегреческий философ, IV в.д.н.э.
Приятно сознавать, что в основе оконного преобразования тоже лежат древнегреческие начала анализа и синтеза.
Владимир Уткин. Уральский геофизик.
Содержание:
Введение.
1. Кратковременное преобразование Фурье. Общий принцип. Частотно-временное оконное преобразование.
2. Функции оконного преобразования в среде Mathcad.
Литература.
Введение
Спектральное представление периодического сигнала комплексным рядом Фурье, а равно и произвольного сигнала на интервале Т, если нас не интересует его поведение за пределами задания, соответствует выражению:
s(t)
=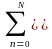 Sn
exp(jtn),
Sn
= (1/T)
Sn
exp(jtn),
Sn
= (1/T) s(t)
exp(-jtn).
s(t)
exp(-jtn).
Ряд Фурье, как правило, является приближенным и ограничивается определенным количеством членов ряда N, обеспечивающем требуемую точность обработки данных.
Сигнал временного интервала, а равно и его Фурье-преобразование, не предоставляет достаточно информации для приложений, которые требуют понимания того, как изменяется частота сигнала во времени. Фурье-преобразование ограничено стационарными сигналами, имеющими фиксированное частотное наполнение. Напротив, нестационарные сигналы требуют методов обработки, которые могут количественно оценивать изменения во времени частотного спектра сигналов, т.е. изучения частотно-временных характеристик сигналов.
Частотно-временной анализ сигналов - одна из последних разработок, которая дает инструментальные средства для изучения и обработки нестационарных сигналов во многих областях науки и техники, таких как передача данных, дефектоскопия, метеорология, биомедицина и др. Есть два основных подхода к гармоническому временному анализу. При первом сигнал разделяется на секторы времени и частотное информационное наполнение вычисляется для каждого из этих секторов отдельно. При втором подходе сигнал сначала фильтруется в различных полосах частот и затем эти полосы частот отображаются в секторы времени. Первый подход - кратковременное оконное Фурье-преобразование, второй – преобразование Wigner-Ville.
С позиций точного представления произвольных сигналов и функций, преобразование Фурье также имеет ряд недостатков, которые привели к появлению оконного преобразования Фурье и стимулировали развитие вейвлетного преобразования. Отметим основные из них:
ограниченная информативность анализа нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей), т.к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков и т.п.) по всему частотному диапазону спектра.
появление эффекта Гиббса на скачках функций, при усечениях сигналов и при вырезке отрезков сигналов для локального детального анализа;
гармонический характер базисных функций, определенных в интервале от - до +.
Неспособность преобразования Фурье осуществлять временную локализацию сингулярностей сигналов может быть частично устранена введением в преобразование так называемой движущейся оконной функции, имеющей компактный носитель. Использование оконной функции позволяет представлять результат преобразования в виде функции двух переменных - частоты и временного положения окна.
