10. Проводники в электростатике (распределение зарядов, картина поля, острия ...)

В проводниках имеются электрически заряженные частицы – носители заряда (электроны в металлах, ионы в электролитах) способные перемещаться по всему объему проводника под действием внешнего электростатического поля.

Носителями заряда в металлах являются электроны проводимости. Они возникают при конденсации паров металла за счет обобществления валентных электронов.

При отсутствии электрического поля металлический проводник является электрически нейтральным – электростатическое поле создаваемое положительными и отрицательными зарядами внутри него компенсируется

• При внесении металлического проводника во внешнее электростатическое поле, электроны проводимости перемещаются (перераспределяются) до тех пор, пока всюду внутри проводника поле электронов проводимости и положительных ионов не скомпенсирует внешнее поле.

• В любой точке внутри проводника, находящимся в электростатическом поле Е = 0; dφ = 0; т. е. φ = const.

• Диэлектрическая проницаемость

• На поверхности проводника напряженность направлена по нормали к этой поверхности, иначе, под действием составляющей E_τ, касательной к поверхности, заряды перемещались бы по проводнику, а это противоречило бы их статическому распределению.

• Вне заряженного проводника – поле есть, следовательно, должен быть вектор , и направлен он перпендикулярно поверхности!

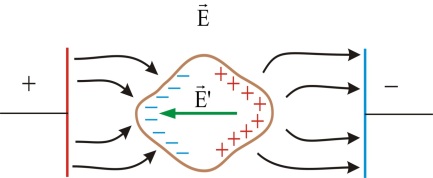
• В установившимся состоянии в проводнике, помещенном в электростатическое поле мы имеем

• Появление у заряженной поверхности на металле заряда противоположного знака – электростатическая индукция. Этот процесс очень краток ~ 10^–8 секунд.

• Электростатическое экранирование – внутрь проводника поле не проникает.

• Во всех точках внутри проводника Е = 0, а во всех точках на поверхности Е = E_n (E_τ = 0);

• Весь объем проводника, находящегося в электростатическом поле эквипотенциален.

• Действительно, в любой точке внутри проводника, следовательно, φ = const.

• Поверхность проводника тоже эквипотенциальна:

(5.1.1)

(для любой линии на поверхности)

• Потенциал поверхности равен потенциалу объема проводника.

• В заряженном проводнике некомпенсированные заряды, располагаются только на поверхности (их расталкивают кулоновские силы).

Доказательство:

Согласно теореме Остроградского – Гаусса суммарный заряд q внутри объема проводника равен нулю, так как Е=0

11. Электроемкость уединенного проводника. Конденсаторы. Электроемкость конденсатора. (примеры: плоский, сферический, цилиндрический конденсатор)

Электрической емкостью уединенного проводника называется его мера способности удерживать электрический заряд.

(15.1)

Емкость определяется геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды. Она не зависит от материала, от агрегатного состояния, от полостей внутри проводника (так как все избыточные заряды снаружи). Наличие вблизи проводника других тел изменяет его емкость, так как потенциал проводника зависит от расположения всех зарядов в пространстве.

2. Единица электроемкости.

Единицей электроемкости является 1 Фарад (Ф).

1 Фарад - единица SI электроемкости, равная емкости такого проводника, который, получая заряд 1 Кулон, изменяет свой потенциал на 1 Вольт.

(15.2)

Koнденсатор

Конденсатором называется устройство, предназначенное для получения нужных величин электроемкости.

Как правило, конденсатор состоит из двух проводящих тел (обкладок), разделенных диэлектриком. Причем его устройство обычно таково, что электрическое поле почти полностью сосредоточено между обкладками. Собственные емкости обкладок малы по сравнению с емкостью конденсатора, которая по определению равна

, (15.3)

где Q- положительный заряд одной из обкладок (на другой обкладке заряд отрицательный), а Dj - разность (или изменение) потенциалов между обкладками.

Если между обкладками не вакуум, а диэлектрик с проницаемостью e, то понятно, что напряженность поля в e раз меньше, разность потенциалов во столько же раз меньше, а емкость, соответственно, больше.

, (15.4)

где С0 -емкость вакуумного конденсатора.

4. Плоский конденсатор.

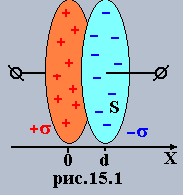
Он представляет собой две бесконечные параллельные пластины площадью S, находящиеся на расстоянии d друг от друга (рис.15.1). Разность потенциалов в этом случае была определена ранее (7.14). Заряд на пластине Q=sS. Тогда емкость

, (15.6)

Строго говоря, если пластины бесконечны, то и площадь их бесконечна. Имеется в виду конденсатор, расстояние между пластинами которого намного меньше характерного размера пластин.

5. Сферический конденсатор.

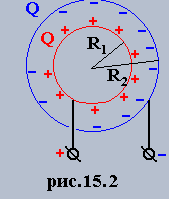
Он представляет собой две проводящие концентрические сферы с радиусами R1<R2. На внутренней сфере заряд +Q, на внешней -Q (рис.15.2). Потенциал на обоих сферах создается как внутренней, так и внешней сферами. Тогда в соответствии с (7.17) потенциал внутренней сферы

а внешней

Следовательно,

(15.9)

Если внешнюю сферу удалить на бесконечность (R2®¥), то емкость уединенной сферы

(15.10)

Отсюда понятно, почему электрическая постоянная измеряется в Фарадах/метр.

Для примера рассчитаем емкость земного шара, приняв его за проводящий шар радиусом Rз=6370 км. Тогда в соответствии с (15.10) емкость Земли Сз=700 мкФ. Очень скромная величина для современных конденсаторов.

Если размеры сфер близки, т.е. R2-R1=d<<R, то

(15.11)

Это и понятно. В этом случае сферический конденсатор вырождается в набор плоских.

6. Цилиндрический конденсатор.

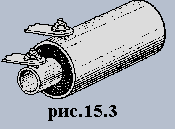
Он представляет две проводящие концентрические очень длинные цилиндрические поверхности с радиусами R1<R2. (рис.15.3) На внутреннем цилиндре заряд +Q, на внешнем -Q. Вспомните, что внутри проводящей цилиндрической поверхности поля нет, поэтому разность потенциалов создается только внутренним цилиндром. Она нам известна (7.22). Заряд цилиндра Q=tl. Тогда

, (15.12)

Если размеры цилиндров близки, т.е. R2-R1=d<<R, то разлагая логарифм в ряд до первого члена, получим

, (15.13)

и емкость конденсатора

, (15.14)

Цилиндрический конденсатор вырождается в набор плоских.