25. Поле прямого тока.

При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии , от контура магнитная индукция будет иметь вид:

Если к прямолинейному проводнику с током поднести магнитную стрелку, то она будет стремиться стать перпендикулярно плоскости, проходящей через ось проводника и центр вращения стрелки (рис. 67).

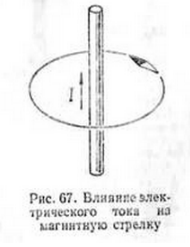
Это указывает на то, что на стрелку действуют особые силы, которые называются магнитными. Иными словами, если по проводнику проходит электрический ток, то вокруг проводника возникает магнитное поле.

Магнитное поле можно рассматривать как особое состояние пространства, окружающего проводники с током.

При расчетах магнитных полей пользуются величиной, называемой напряженностью магнитного поля (обозначается Н). Магнитная индукция В и напряженность магнитного ноля Н связаны соотношением:

Единица измерения напряженности магнитного поля ампер на метр (А/м).

Напряженность магнитного поля в однородной среде, так же как и магнитная индукция, зависит от величины тока, числа и формы проводников, по которым проходит ток. Но в отличие от магнитной индукции напряженность магнитного поля не учитывает влияния магнитных свойств среды.

26. Взаимодействие параллельных токов. Определение на этой основе единицы силы тока.

Как нам уже известно, магнитное поле оказывает на рамку с током ориентирующее действие. Значит, вращающий момент, который испытывает рамка, является результатом действия сил на отдельные ее элементы. Сравнивая и обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер открыл, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, который находится в магнитном поле, равна   (1)  где dl - вектор, по модулю равный dl и совпадающий по направлению с током, В - вектор магнитной индукции.  Направление вектора dF может быть определено, используя (1), по правилу векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, которая действуюет на ток.  Модуль силы Ампера (см. (1)) равен   (2)  где α — угол между векторами dl и В.  Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Магнитное поле тока I1 есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B1 задается правилом правого винта, его модуль по формуле (5) есть    Направление силы dF1, с которой поле B1 действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I2 и вектором B1 прямой, будет равен    подставляя значение для В1, найдем   (3)  Аналогично рассуждая, можно показать, что сила dF2 с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна   (4)  Сопоставление выражений (3) и (4) дает, что    т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной   (5)  Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5).