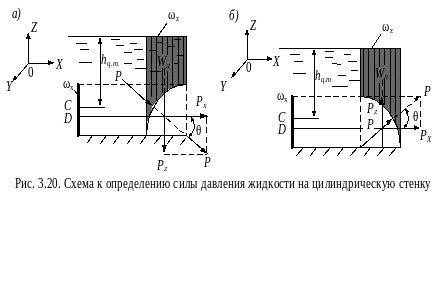
12. Давление жидкости на цилиндрические стенки

Рассмотрим некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой. Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости, которое сводится к тому, что в каждой точке на стенку действует давление жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими и выразим элементарную силу давления на них в общем виде dP = pd. Силы dP уже не будут направлены параллельно друг другу, их линии действия могут не пересекаться в одной точке, и их сумма может не сводиться к одной равнодействующей.

Для шаровой или круговой цилиндрической стенки элементарные силы давления направлены по радиусам, пересекутся в центре сферы или в центре круга.

Цилиндрическая поверхность с горизонтальной образующей.

Значение силы давления на цилиндрическую поверхность определяется:

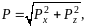где Р_х и Р_z – горизонтальная и вертикальная составляющие силы давления. Горизонтальная dP_x и вертикальная dP_у составляющие силы dP:

для горизонтальной составляющей силы Р: 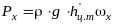, где _х – проекция всей цилиндрической поверхности на плоскость, нормальную к оси ОХ;

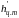– глубина центра тяжести проекции _х под пьезометрической плоскостью.

Для вертикальной составляющей получим: .

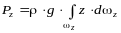13. Закон архимеда

Рассмотрим полностью погруженное в жидкость твердое тело, объем которого W_т, а форма такова, что любая прямая пересекает поверхность этого тела только в двух точках (рис. 3.21). Для определения силы Р давления жидкости на тело воспользуемся результатами предыдущего пункта.

Горизонтальные составляющие силы Р_х и Р_у взаимно уравновеши­ваются. Вертикальная составляющая силы давления Р_z равна весу жидкости в объеме тела.

Действительно, в данном случае имеем два тела давления: ABMNAEF, соответствующее давлению на верхнюю часть тела, и AKMFE, соответствующее давлению на нижнюю часть тела. Объем первого тела давления равен W₁, объем второго тела давления W₂, причем W₂ = W₁ + W_т.

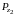Вертикальная составляющая , равна весу жидкости в объеме W₁, то есть gW₁, и направлена по вертикали вниз. Вертикальная составляющая , равна весу жидкости в объеме W₂, то есть gW₂, и направлена по вертикали вверх.

Равнодействующая сила давления равна разности указанных составляющих:

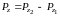
_или

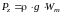
Силу P_z называют архимедовой силой.

Так как Р_х = Р_у = 0, то Р = Р_z.

С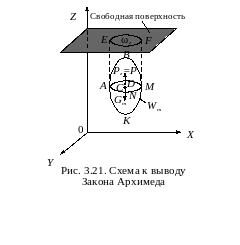 ила давления покоящейся жидкости на погруженное в нее тело –архимедова сила – равна весу жидкости gW в объеме, вытесненном телом, направлена по вертикали вверх и приложена в центре тяжести этого объема. Это и есть закон Архимеда.

14. Два метода изучения движения жидкости

Способ Лагранжа. В этом способе предлагается рас­сматривать движение каждой частицы жидкости. В началь­ный момент времени положение частицы определено на­чальными координатами ее полюса x₀, y₀, z₀. При движении частица перемещается и координаты ее полюса изменяют­ся. Движение жидкости определено, если для каждой час­тицы можно указать координаты x, y, z как функции на­чального положения x₀, y₀, z₀ и времени t: 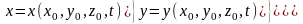Переменные x₀, y₀, z₀ и t называют переменными Лагранжа. Совокупность приведенных функций описывает траектории движений частиц жидкости. Из урав­нений можно найти проекции на координатные оси скоростей и ускорений всех жидких частиц. Если обозна­чить через и вектор скорости жидкой частицы, то проекции скорост 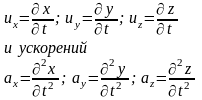При описании движ жид методом Лагранжа можно пользоваться также криволинейными координатами.

Метод Эйлера В этом способе движение жидкости описывается функциями, выражающими изменения скорос­тей в точках некоторой неподвижной области, выбранной в пределах потока. В данный момент времени в каждой точ­ке этой области, определяемой координатами х, у, z, нахо­дится частица жидкости, имеющая некоторую скорость u.

Эта скорость называется мгновенной местной скоростью. Совокупность мгновенных местных скоростей представляет векторное поле, называемое полем скоростей. В общем случае поле скоростей может изменяться во времени и по координатам:

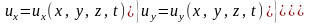Переменные x, y, z, t на­зывают переменными Эйлера. По характеру изменения поля скоростей во времени движения жидкости делятся на неустановившиеся и установившиеся.

Неустановившееся (нестационарное) движение такое, когда в точках области, где движется жидкость, местные скорости изменяются с течением време­ни. Такое движение описывается уравнениями (3.4).

При неустановившемся движении в общем случае линии тока соответствуют только мгновенному состоянию поля скоростей. В последующие моменты времени поле скорос­тей и, следовательно, линии тока могут изменяться. В связи с этим в общем случае при неустановившемся движении линии тока и траектории могут не совпадать. Но может встретиться частный случай неустановившегося движения, когда направление и форма линий тока не изменяются во времени (направления скоростей остаются неизменными, изменяются только значения скоростей и в точках). В этом случае линии тока и траектории частиц жидкости совпадут.

Установившееся (стационарное) движение такое, когда в каждой точке области, где движется жидкость, местные скорости во времени не изменяются, Тогда уравнения превращаются в следующие: