1 Физические свойства жидкостей. Текучесть. Если к участку жид, находящейся в равновесии, приложить внешнюю силу, то возникает поток частиц жид в том направлении, в котором эта сила приложена: жид течёт. Таким образом, под действием неуравновешенных внеш сил жид не сохраняет форму и относительное расположение частей, и поэтому принимает форму сосуда, в котором находится. В отличие от пластичных твёрд тел, жид не имеет предела текучести: достаточно приложить сколь угодно малую внеш силу, чтобы жид потекла. Вязкость. Она определяется как способ оказывать сопрот. перемещению одной из частей относительно др –т.е. как внутр. трение. Когда соседние слои жид движ относительно друг др, неизбежно происх столкновение молекул дополнительно к тому, которое обусловлено тепловым движ. Возникают силы, затормаживающие упорядоченное движ. При этом кинет.энергия упорядоченного движ переходит в тепловую — энергию хаотического движ молекул. Жид в сосуде, приведённая в движ и предоставленная самой себе, постепенно остановится, но её t повысится. Испарение и конденсация. Испар — постепенный переход вещества из жидкости в газообразную фазу. При тепловом движ некоторые молекулы покидают жид через её поверх и переходят в пар. И часть молекул переходит обратно из пара в жид. Если из жид уходит больше молекул, чем приходит, то имеет место испарение. Конденсация — обратный процесс, переход вещ-ва из газообразного состояния в жид. Испарение и конденсация — неравновесные процессы, они происходят до тех пор, пока не установится локальное равновесие, причём жид может полностью испариться, или же прийти в равновесие со своим паром, когда из жид выходит столько же молекул, сколько возвращается. Кипение  — процесс парообразования внутри жид-ти. При достаточно высокой t давление пара становится выше давления внутри жид, и там начинают образовываться пузырьки пара, которые всплывают наверх. Смачивание - поверхностное явление, возник-ее при контакте жид с тв поверх-ю в присутствии пара, т.е на границах раздела трёх фаз. Смачивание характеризует «прилипание» жид к поверхности и растекание по ней. Различают три случая: несмачивание, ограниченное смачивание и полное смачивание. Смешиваемость – способ жид-ей растворяться друг в др. Диффузия. При нахождении в сосуде двух смешиваемых жид молекулы в результате теплового движ начинают постепенно проходить через поверх раздела, и таким образом жид постепенно смешиваются, называется диффузией. Перегрев и переох, Волны плотности, Сосуществование с др фазами.

2. Классификация сил, действующих в жидкости

По характеру действия силы можно разделить на две категории: массовые силы и поверхностные. Массовые силы. Силы, действующие на каждую частицу жидкости с массой М = V, то есть силы, распределенные по массе, называются массовыми. К ним относятся: сила тяжести, силы инерции, гравитационные силы, подчиняющиеся закону всемирного тяготения Ньютона. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой ΔM = ρV действует сила ΔF, в зависимости от ее массы. Пусть объем ΔV содержит в себе точку А. Тогда в точке А: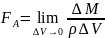 , где FА – плотность силы в элементарном объеме. Плотность массовой силы – векторная величина, отнесена к единичному объему ΔV; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. Т.е плотность массовой силы ведет себя, как массовая сила. Поверхностные силы. Силы, действующие на каждый элемент  поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называются поверхностными. Поверхностные силы делятся на две группы: нормальные и касательные. К нормальным поверхностным силам относится сила давления Р, к касательным относится сила трения Т.

Если по аналогии определить плотность этих сил, то: нормальное напряжение в точке А: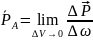 , касательное напряжение в точке А: 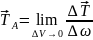. И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.

3.Свойства напряжений поверхностных сил

Очевидно, что , с учетом чего связь между напряжениями запишется в виде:

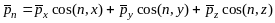. Первое свойство: напряжения поверхностных сил, действующих по произвольной площадке в данной точки жидкости, зависят от девяти скалярных величин: трех нормальных напряжений (р_хх, р_уу, p_zz) и шести касательных (_ху, _xz, _yz, _yx, _zx, _zy). Такие величины в математике и механике носят название тензора, таким образом первое свойство напряжений поверхностных сил состоит в том, что эти напряжения образуют тензор напряжений.

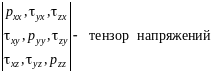. Нормальные и касательные напряжения, действующие на три взаимно перпендикулярные грани параллелепипеда, выделенные в жидкости.

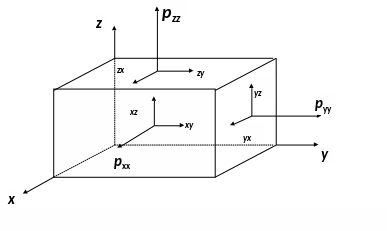
Применяя теорему моментов, взятых относительно начала координат для напряжений, действующие на грани параллелепипеда, можно доказать свойство взаимности касательных напряжений, в соответствии с которым: 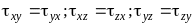. Из этого следует, что вследствие взаимности число независимых величин сокращается до шести. Эти равенства позволяют сформулировать теорему о свойстве нормальных напряжений: Второе свойство: если в жидкости отсутствуют касательные напряжения, то нормальные напряжения в данной точке не зависят от ориентации площадки. Третье свойство: капельная жидкость способна воспринимать произвольные сжимающие усилия (отрицательное нормальное напряжение) без разрыва сплошности. Однако жидкость практически терпит разрыв при растяжении, то есть в ней могут провялятся лишь нормальные сжимающиеся усилия.

Назовем давлением р в жидкости при отсутствии касательных напряжений величину нормального напряжения, взятую с обратным знаком, тогда, в соответствии с только что доказанной теоремой 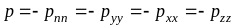, отсюда следует, что величина давления не зависит от ориентации площадки.

4. Уравнения движения жидкости в напряжениях. Запишем уравнение дви­жения этой частицы, обозначая ускорение ее центра тяжести 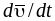: 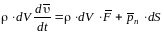Подставляя правую часть в уравнение, получим:

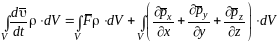. Все члены в этом уравнении интегрируются по объему. Это уравнение является уравнением движения жидкого объема в интегральной форме. Левая часть представляет главный вектор сил инерции, первый член правой части – главный вектор массовых сил, а второй – главный вектор поверхностных сил. Получим дифференциальное уравнение движения жидкости в напряжениях:

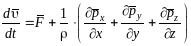, которое связывает ускорение с напряжениями массовых и поверхностных сил в данной точке потока и справедливо как для вязкой, так и невязкой жидкости.

Проектируя векторное уравнение на оси координат, будем иметь: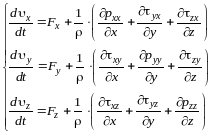 Эта система уравнений служит для разработки гидростатики и гидродинамики вязкой и невязкой жидкости.