2. Формула Тейлора с остаточным членом в форме Пеано.
Пусть имеется f(x), имеющая производные до n-го порядка. Поставлена задача найти многочлен Pn(x):
Pn(x0) = f(x0), P’n(x0) = f’(x0), P’’n(x0) = f’’(x0), … , P(n)n(x0) = f(n)(x0). (1)
Этот многочлен был найден в виде:
Pn(x) = f(x0) + (x – x0) + … + (x – x0)n = (x – x0)k. (3)
Теорема 7.14. Пусть функция f(x) n раз дифференцируема в точке x0, тогда для функции f(x) имеет место равенство:
f(x) = Pn(x) + o((x – x0)n), где Pn(x) – многочлен Тейлора для функции f(x).
Доказательство.
Введем обозначение:
R(x)=f(x)-Pn(x)=f(x)–[f(x0)+
(x–x0)+
… +
(x–x0)n-1+
(x–x0)n].
Надо доказать, что R(x) = o((x – x0)n). Мы докажем это с помощью правила Лопиталя.
Требуется доказать,
что
=
0. (5)
Отметим прежде всего, что в силу условия теоремы сама функция f(x) и ее производные f’(x), … , f(n-1)(x) непрерывны в точке x0. Поэтому, используя условие (1), получаем:
R(x) = [ f(x) - Pn(x)] = f(x0) - Pn(x0)] = 0. (6)
R’(x) = [ f’(x) – P’n(x)] = f’(x0) – P’n(x0)] = 0. (6’)
и так далее…
R(n-1)(x) = [ f(n-1)(x) – P(n-1)n(x)] = f(n-1)(x0) – P(n-1)n(x0)] = 0. (6(n-1))
В силу (6) предел
(5) является неопределенностью типа
.
В силу (6’)
также является неопределенностью типа
.
и так далее…
В силу (6(n-1))
=
снова является неопределенностью типа
.
Для вычисления последнего предела
рассмотрим выражение для R(n-1)(x).
R(n-1)(x)
= f(n-1)(x)
- f(n-1)(x0)
- f(n)(x0)(x
– x0).
Так как f(n-1)(x)
дифференцируема в точке x0,
то ее приращение в точке x0
тожно представить в виде:
f(n-1)(x)
- f(n-1)(x0)
=
(x
– x0)
+ o(x
– x0)
= f(n)(x0)(x
– x0)
+ o(x
– x0).
Следовательно,
R(n-1)(x)
= o(x
– x0),
поэтому
=
=
0.
Таким образом, применяя к пределу (5) правило Лопиталя, получим:
= = … = = 0,
что и требовалось доказать.
Теорема доказана.
Введем обозначение: Rn+1(x) = R(x) = f(x) - Pn(x). Тогда равенство (4) можно записать в виде:
f(x) = Pn(x) + Rn+1(x), (4’)
где Rn+1(x) = o((x – x0)n).
Функция Rn+1(x) называется остаточным членом, а формула (4) называется формулой Тейлора для функции f(x) с центром разложения в точке x0 и с остаточным членом в форме Пеано.
Формула Тейлора с остаточным членом в форме Лагранжа.
Многочлен Тейлора.
Если f(x) дифференцируема в точке x0, то ее приращение в этой точке можно представить в виде:
f(x) - f(x0) = f’(x0)(x – x0) + o(x – x0).
f(x) = + o(x – x0).
P1(x) обладает следующими свойствами: P1(x0) = f(x0), P’1(x0) = f’(x0). Рассмотрим теперь более общую задачу. Пусть f(x) n раз дифференцируема в точке x0, то есть имеет в точке n все производные до n-го порядка. Поставим задачу найти такой многочлен Pn(x) (степени n), что:
Pn(x0) = f(x0), P’n(x0) = f’(x0), P’’n(x0) = f’’(x0), … , P(n)n(x0) = f(n)(x0). (1)
Будем искать многочлен Pn(x) в виде:
Pn(x) = a0 + a1(x – x0) + a2(x – x0)2 + a3(x – x0)3 + … + ak(x – x0)k + … + an(x – x0)n. (2)
Покажем, что можно так выбрать коэффициенты a0, a1, … , an, что многочлен Pn(x) будет удовлетворять условию (1). Полагая в равенстве (2) x = x0 и учитывая первое из равенств (1), получим Pn(x0) = a0 = f(x0). a0 = f(x0). Продифференцируем равенство (2).
P’n(x) =a1 + 2a2(x – x0) + 3a3(x – x0)2 + … + nan(x – x0)n-1. (2’)
Положим в равенстве (2’) x = x0 и учтем второе условие из (1).
P’n(x0) =a1 = f(x0).
a1 = .
Продифференцируем равенство (2’):
P’’n(x) = 2a2 + 23a3(x – x0) + … + n(n – 1)an(x – x0)n-1. (2’’)
Положим в полученном равенстве (2’’) x = x0 и учтем третье условие из (1).
P’’n(x0) = 2a2 = f’’(x0).
a2 = .
И так далее. После k –кратного дифференцирования равенства (2) получим:
P(k)n(x) = k!ak + 2ak+1(x – x0) + … + n(n - 1)…(n – k + 1)(x – x0)k. (2(k))
Полагая здесь x = x0 и учитывая k+1–е условие из (1), получим:
P(k)n(x0) = k!ak = f(k)(x0).
ak = (k = 0, 1, … , n), если принять обозначения f(0) = f, 0! = 1. Итак, мы нашли такие коэффициенты ak, что многочлен
Pn(x) = f(x0) + (x – x0) + … + (x – x0)n = (x – x0)k. (3)
удовлетворяет условиям (1). Многочлен (3) называется многочленом Тейлора для функции f(x).
Теорема 7.15. Пусть f(x) определена и n+1раз дифференцируема в окрестности точки x0. Пусть x – любое значение аргумента из этой окрестности, не равное x0, p – любое вещественное число. Тогда точка (x0, x):
Rn+1(x)
= f(x)
– Pn(x)
=
. (7)
Равенство (7) называется остаточным членом в общей форме.
Доказательство.
Введем обозначение: Pn(x) = f(x0) + … + (x – x0)n (x, x0). Возьмем x x0 из указанной в условии теоремы окрестности точки x0. Пусть для определенности x > x0.
(здесь рисунок)
x – фиксированное. Возьмем какое-нибудь p > 0. Числовую переменную, изменяющуюся на сегменте [x0, x], обозначим буквой t: x0 t x, и введем функцию:
(t)
= f(x)
- (x,
t)
-
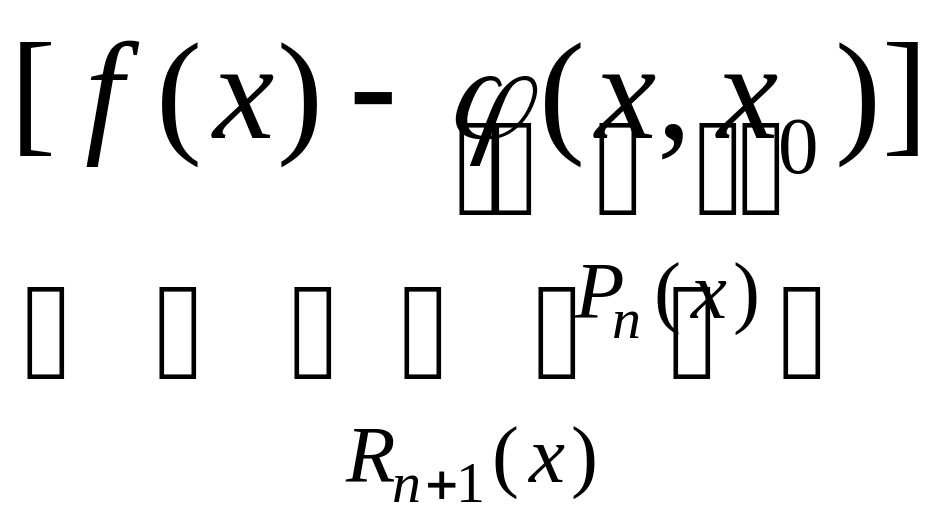= f(x)
- (x,
t)
-
Rn+1(x).
(t) на [x0, x] удовлетворяет всем условиям теоремы Ролля:
(t)
= f(x)
- [f(t)
+
(x
– t)
+
(x
– t)2
+ … +
(x
– t)n]
-
Rn+1(x).
Так как f(x) n+1 раз дифференцируема, то (t) непрерывна на [x0, x],
(t) дифференцируема в интервале (x0, x),
(x0) = f(x) - (x, x0) -
[
f(x)
- (x,
x0)]
= 0,
(x) = 0, (x0) = (x). По теореме Ролля, (x0, x): ’() = 0.
’(t)
= - [f’(t)
- f’(t)
+ f’’(t)(x
– t)
- f’’(t)(x
– t)
+
(x
– t)2
- …
+ … -
(x
– t)n-1+
+
(x
– t)n]
+ p
Rn+1(x).
Полагая t = , получаем:
’()
=
(x
– )n
+ p
Rn+1(x)
= 0.
Rn+1(x) = . (7)
Теорема доказана.
Следствия.
p = n + 1.
Rn+1(x)
=
(x
– x0)n+1 (8)
Это остаточный член в форме Лагранжа.
(здесь рисунок)
- x0 = (x – x0), 0 < < 1.
= x0 + (x – x0).
Rn+1(x)
=
(x
– x0)n+1. (8)
p = 1. Тогда Rn+1(x) =
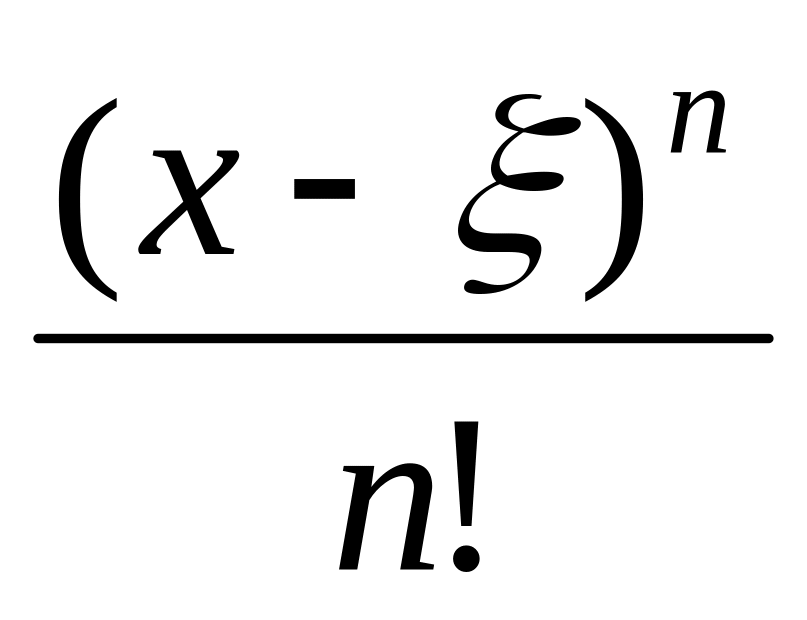(x
– x0)f(n+1)().
Т.к.
= x0
+ (x
– x0),
то x
-
= (x
– x0)(1
- ).
Rn+1(x)
=
(1-)n
f(n+1)(x0
+ (x
– x0)). (9)
Это остаточный член в форме Коши.
Разложение по формуле Маклорена функции ln(1 + x).
Формулой Маклорена называется формула Тейлора с центром в точке a = 0. Формула Маклорена дает представление функции в окрестности точки x = 0. Запишем формулу Маклорена для произвольной функции f(x) с остаточным членом в форме Лагранжа, Коши и Пеано.
(1)
где остаточный член имеет вид:
в форме Лагранжа
(2)
в форме Коши
(3)
( в формулах Лагранжа и Коши, вообще говоря, различные)
в форме Пеано
(4)
Рассмотрим
разложение
по формуле Маклорена.
При n 1
(5)
где остаточный член имеет вид:
в форме Лагранжа
(6)
в форме Коши
(7)
в форме Пеано
(8)
Оценки остаточного члена:
в форме Лагранжа
0 x 1. Переходя в (6) к модулям
при 0
x
1 (9)
в форме Коши
-r x 0, где 0 < r < 1. Переходя в (7) к модулям
т.к. 0 <
r
< 1 (10)