6. Надежность элементов. Случайные величины и их характеристики

Случайная величина - величина, которая может принимать одно из заранее известных значений. В теории надежности случайными величинами является:

1. Ресурс, наработка до отказа, число отказов за период эксплуатации.

Случайная величина может быть непрерывной или дискретной. Случайная величина называется непрерывной, если она может принимать конечное или бесконечное количество, которое можно пронумеровать.

Возникновение отказов машин и оборудования зависит от большого числа различных факторов: высокая температура, значительные динамические нагрузки, неравномерность физических и механических свойств обрабатываемых деталей и т.д., поэтому все отказы носят случайный характер, а сам отказ необходимо трактовать, как случайную величину. Для оценки случайной величины необходимо знать ее закон распределения - зависимость между возможными значениями случайной величины и вероятностями их появления. Закон распределения случайной величины F(x), который в теории надежности называют инструментальной функцией распределения. Она определяет вероятность того, что в результате испытаний случайная величина Х не превысит некоторое значение х. в теории надежности изменение случайной величины Х находится в интервале от 0 до 1, а аргумент функции F(x) обычно является время. Производная от функции распределения называется плотностью распределения обозначения f(x):

f(x)=dF(x)/d(t)

2. Математическое ожидание случайной величины.

Математическое ожидание

M(t)=∑t_i/n,

t_i - значение случайной величины;

n - количество наблюдений.

Дисперсия случайной величины - это математической ожидание квадрата отклонения от ее математического ожидания.

Аналогично вводят характеристику среднеквадратичного отклонения

7. Экспоненциальный закон распределения

1. Для экспоненциального закона одной из основных характеристик является плотность распределения наработки, которая рассчитывается по формуле:

- интенсивность отказа, т.е. величина, определяющая количество отказов в единицу времени.

2. P(t) - вероятность безотказной работы: ; P(t)=1-Q(t).

3. Средняя наработка до отказа:

4. Среднее квадратичное отклонение:

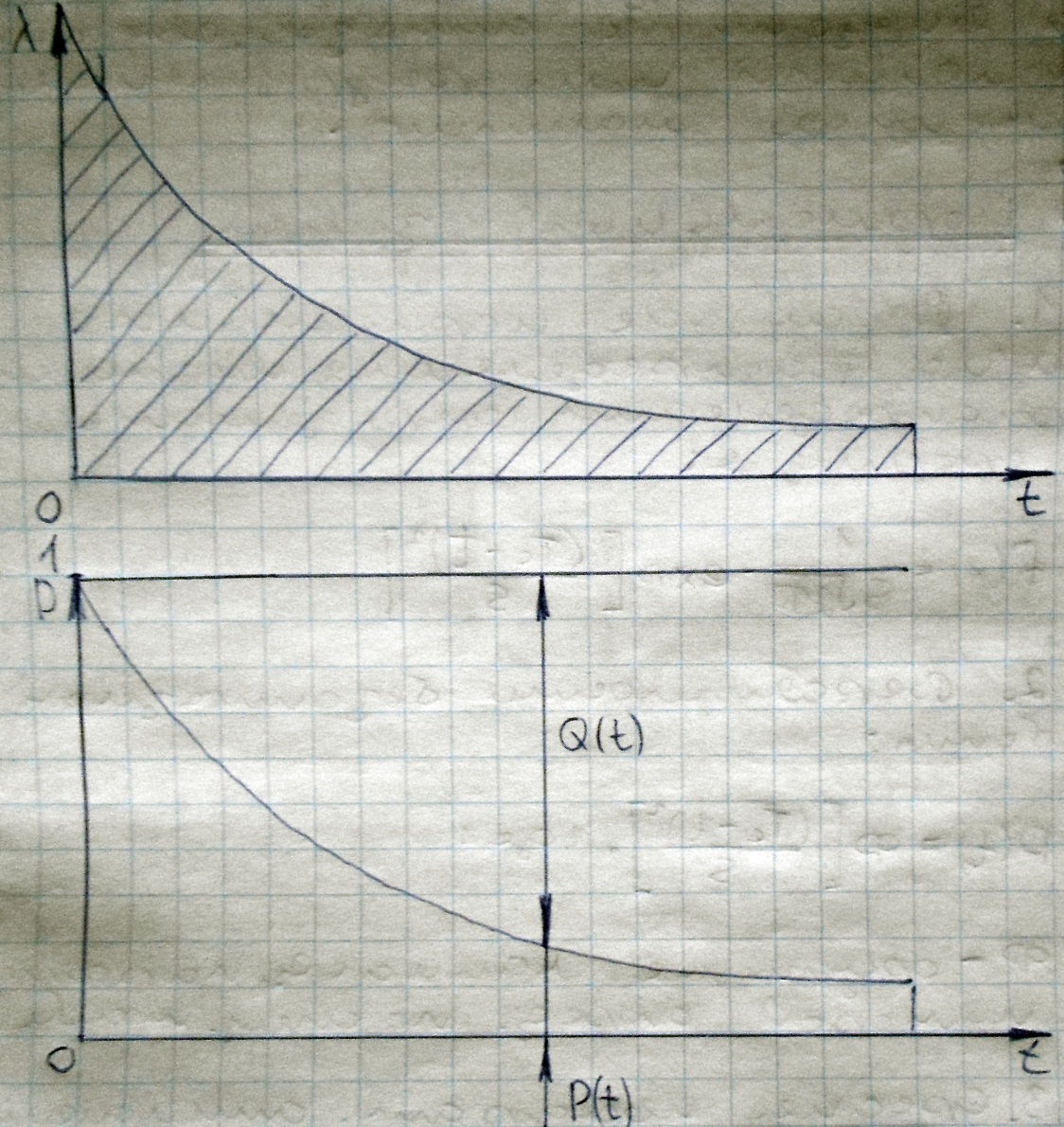
При экспоненциальном законе распределения интенсивность отказов является величиной постоянной, обратно пропорциональной наработке до отказа. Это означает, что испытание объекта до некоторого значения t не влияет на остаточное время безотказной работы. Это значит, что объект не стареет.

Данный закон распределения применим для внезапных отказов, связанных с поломками и разрушением объекта.

8. Нормальный закон распределения

1. В случае нормального закона распределения плотность распределения определяется по формуле:

2. Вероятность безотказной работы:

Ф – функция Лапласа, параметры которой определяются по таблице.

3. Среднее квадратичное отклонение:

Графически нормальный закон распределения можно представить следующим образом:

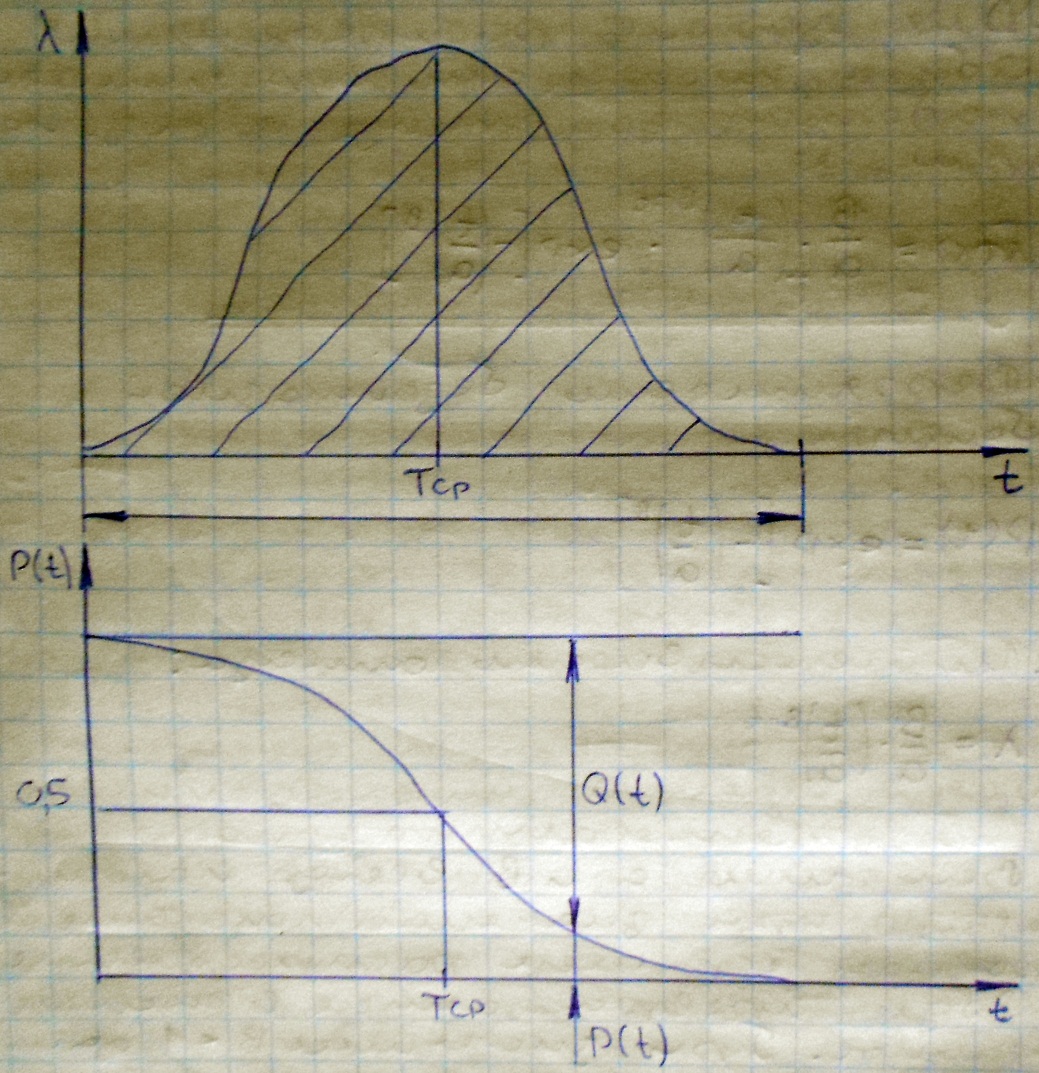
Нормальный закон распределения характерен для постепенных отказов обусловленных износом и старением, с хорошей точностью описывает результаты анализа сложных с учетом изменения параметров в процессе эксплуатации.