7.2. Выборочная дисперсия

По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой (приближенным значением) генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии. Выборочная дисперсия   для выборки, состоящей из случайных величин  , определяется следующим образом: Используя это представление выборочной дисперсии, найдем ее математическое ожидание Таким образом, мы получили, что  . Это значит, что выборочная дисперсия является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку, нужно величину  умножить на   тогда  и выборочная дисперсия   принимает вид: = Итак, мы получили следующий результат. Если в результате n независимых измерений случайной величиныХ с неизвестным математическим ожиданием и дисперсией нам нужно по полученным данным определить эти параметры, то следует пользоваться такими оценками: В случае, если известно математическое ожидание генеральной совокупности mx, то выборочную дисперсию следует вычислять по формуле = которая также является несмещенной оценкой. Относительной оценкой степени разброса случайной величины Х по отношению к выборочному среднему является коэффициент вариации Vстатистического распределения выборки: . Часто по выборочным данным нужно знать оценки таких параметров генеральной совокупности как:центрального (начального) момента k – го порядка, коэффициента асимметрии As, эксцесса Ех.  Выборочным центральным (начальным) моментом k – го порядка   ( )называют величину ( ) Для оценки отклонения статистического распределения выборки от нормального распределения используют числовые характеристики - выборочный коэффициент асимметрии   и выборочный эксцесс . Выборочным коэффициентом  называют число, которое вычисляется по формуле: . Выборочным эксцессом  статистического распределения называют число 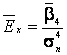. Заметим, что представленные формулы записаны с использованием статистического ряда. В случае интервального вариационного ряда эти формулы преобразуются путем введения весов, равных частоте появления варианты хj. Эти характеристики называются взвешенными числовыми характеристиками. Таквзвешенный центральный (начальный) момент k – го порядка  будет иметь вид:  ( ), где nj – частота варианты xj ( )

29 Точечные оценки, их свойства, примеры

Определение 1.   Выборка -- последовательность результатов измерений значений случайной величины.

Определение 2.   Статистическая оценка -- приближенное значение вероятностных характеристик законов распределения, полученных на основе статистических или выборочных данных. Точечная статистическая оценка -- статистическая оценка, выражаемая одним числом.

Определение 3.   Статистическая оценка называется несмещенной, если  .

Определение 4.   Точечная оценка называется состоятельной, если  .

Определение 5.   Точечная оценка называется сильно состоятельной, если  .

Определение 6.   Точечная оценка   называется эффективной, если  , где   -- все возможные точечные оценки.

Определение 7.   Точечная оценка называется асимптотически эффективной, если

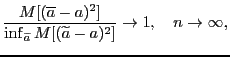
где   -- все возможные точечные оценки.

Пример: выборочное математическое ожидание.  .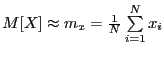

Определение 8.   Пусть   -- оценка параметра  . Мы хотим, чтобы  , т.е. чтобы она была достаточно хорошей, была очень близка к реальному значению в очень большом количестве случаев (95%, 99%). Тогда   -- точность,   -- надежность.

30 Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Метод доверительных интервалов разработал американский статистик Ежи Нейман, исходя из идей английского статистика Рональда Фишера^{[ссылка 1]}.

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100p%^{[примечание 1]}, порождённым выборкой (x₁,…,x_n), называется интервал с границами  (x₁,…,x_n) и  (x₁,…,x_n), которые являются реализациями случайных величин L(X₁,…,X_n) и U(X₁,…,X_n), таких, что

.

Граничные точки доверительного интервала   и   называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.^{[ссылка 2]}

Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.

Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.

Определение

Пусть   - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа   и   такие чтобы выполнялось неравенство:

Интервал   является доверительным интервалом для параметра  , а число   - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

• 31 Интервальная оценка для среднего квадратического отклонения нормально распределенной случайной величины.

Пусть по выборке объема n получено значение s, которое является исправленным средним квадратическим отклонением и  точечной оценкой среднего квадратического отклонения случайной величины Х. Определим величину доверительного интервала для среднего квадратического отклонения.  По определению. Доверительный интервал с заданной надежностью ? имеет вид: . Преобразуем данное выражение. Получим: . Обозначим   через q и, подставив его в это выражение, получим:

• При q < 1         

• При q > 1            

Величина q = q (n,?) находится по специальной таблице. Случайная величина q имеет распределение, зависящее только от n  и  ?, и ее значения табулированы.

Рассмотрим пример из предыдущей лекции. По результатам исследования роста были получены следующие данные:

1. Среднее значение роста

2. Выборочная дисперсия

3. Среднее квадратическое отклонение выборки:

4. Исправленная дисперсия

5. Исправленное среднее квадратичное отклонение

Вычислим для этого примера доверительный интервал для математического ожидания в случае, когда ? известна и равна 10, когда ? неизвестна, доверительный интервал для ? с надежностью 0,95.

•  ? = 10.

По таблице для ? = 0,95 находим, что t?  = 1,96. Находим ?. Записываем ответ: 167,6 – 3,58 < а < 167,6 + 3,56 164,02 < a < 171,16

• Если ? неизвестна, то по таблице для ? = 0,95 и n = 30 t? = 2,05.

  Записываем ответ:  164,13 < а < 171,16

•  По таблице для ? = 0,95 и n = 30 находим q.

q = 0,28 Находим величину доверительного интервала  для q < 1: 9,28 · ( 1 – 0, 28 ) < ? < 9,28 · ( 1 + 0, 28 ) 6,68 < ? < 11,88.

32 Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, – точечные. При выборке малого объёма точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. ^ Пусть найденная по данным выборки статистическая характеристика   служит оценкой неизвестного параметра  ^ . Будем считать   постоянным числом (  может быть случайной величиной). Ясно, что   тем точнее определяет параметр  , чем меньше абсолютная величина разности  ^ . Другими словами, если   > 0 и   то, чем меньше , тем оценка точнее. Таким образом, положительное число   характеризует точность оценки. Однако, статистические методы не позволяют категорически утверждать, что оценка   удовлетворяет неравенству  , можно лишь говорить о вероятности  , с которой это неравенство осуществляется. Надежностью (доверительной вероятностью) оценки   по   называют вероятность , с которой осуществляется неравенство  ^. Обычно надежность оценки задается наперед, причем в качестве   берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

33.Проверка гипотезы о нормальном распределении генеральной совокупности

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины – критерия согласия. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: Пирсона К., Колмагорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона и проверки гипотезы о нормальном распределении генеральной совокупности. С этой же целью будем сравнивать эмпирические (наблюдаемые) и теоретические частоты (вычисленные в предположении нормального распределения). Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Возможно, что расхождение случайно и объясняется малым числом наблюдений либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данным наблюдением. Пусть по выборке объема n получено эмпирическое распределение: варианты xi – x1 x2 xs, эмпирические частоты ni – n1 n2 ns. Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты ni’. При условии значимости a требуется проверить нулевую гипотезу о нормальном распределении генеральной совокупности. В качестве критерия проверки нулевой гипотезы   примем случайную величину, где ni –эмпирические частоты, ni’- теоретические частоты. Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределения. Доказано, что при n®¥ закон распределения случайной величины независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения c²с k степенями свободы. Поэтому случайная величина обозначена через c², а сам критерий называют критерием согласия “хи квадрат”. Число степеней свободы находят по равенству k=s-1-r, где          s – число групп (частичных интервалов) выборки;                 r – число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение). Поэтому r = 2 и число степеней свободы  k=s-1-r =s-1-2=s-3. Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр. Поэтому r = 1 и k=s-2. Поскольку односторонний критерий более "жестко" отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости a. P(c²>c²кр(a;k))=a. Таким образом, правосторонняя область определяется неравенством c²>c²кр(a;k), а область принятия нулевой гипотезы – неравенством c²>c²кр(a;k).