7.6. Симплексный метод решения задачи линейного программирования

Еще одним общим методом решения задач линейного про­граммирования является симплексный метод (симплекс-ме­тод), или метод последовательного улучшения оценок, разрабо­танный Дж. Данцигом (США, 1947).

Геометрическая идея этого метода проста и состоит в следую­щем. Пусть имеется п переменных х1, х₂, ..., х_п и р < n ограни­чений. Область допустимых решений, задаваемая ограничени­ями, представляет собой выпуклый многогранник. Если задача линейного программирования имеет оптимальное решение х*, то оно совпадает с опорной точкой, являющейся одной из вершин многогранника, где, по крайней мере, к = п — р переменных рав­ны нулю. Симплекс-метод заключается в таком направленном переборе вершин многогранника, при котором значение целевой функции возрастает от одной вершины к другой. Переходя по­следовательно из одной опорной точки в другую (изменяя пере­менные) и постепенно улучшая решение, находим оптимальное. Каждой вершине соответствует система уравнений, выбираемых специальным образом из ограничений.

Поясним идею симплекс-метода на примере.

П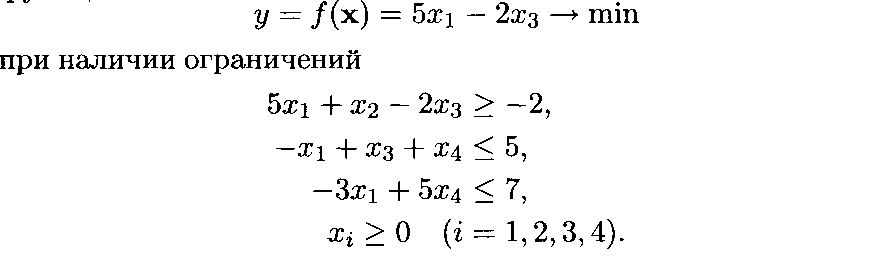 ример 7.4• Требуется минимизировать значение линейной функции

1. Приведем задачу линейного программирования к стандарт­ной форме. Заменим критерий оптимальности и введем дополнительные переменные

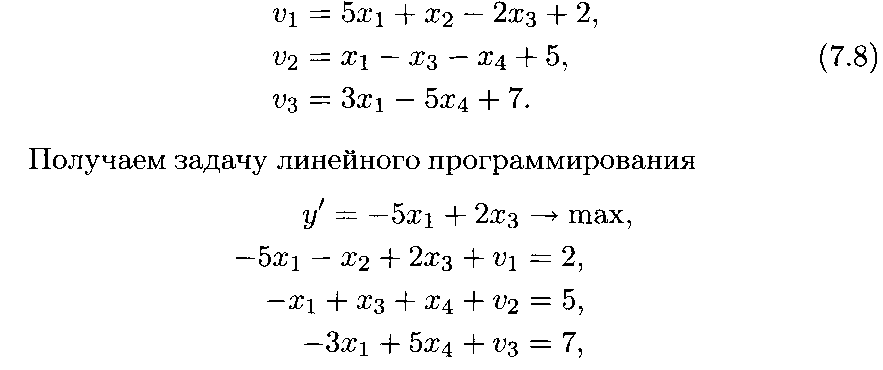
в которой имеется n = 7 неотрицательных переменных x1, х₂, хз, x4, v1, v2, v3 и р = 3 уравнений-ограничений (7.8). Число свобод­ных переменных к = п — р = 4. Переменные х₂, Х4, v1, v2, v3 вхо­дят в функцию у' с нулевыми коэффициентами.

1. Выберем переменные х1,х₂,хз,х4 в качестве свободных и выразим все остальные переменные через них. Эти уравнения (7.8) для переменных v1, v2, v3 записаны выше.

2. Положим все свободные переменные равными нулю: х1 = Х2 = хз = Х4 = 0. Тогда из уравнений (7.8) имеем v1= 2, v₂ .= 5, V3 = 7. Получаем опорное решение, для которого у' = 0. Проверим, является ли это значение у' оптимальным.

Если бы в выражении для критерия оптимальности у' все ко­эффициенты при переменных Хi были отрицательными, то уве­личить значение у', повышая значения переменных хi, было бы нельзя. И сразу получили бы оптимальное значение у' *. Однако в выражении для функции у' коэффициент при переменной х3 положителен. Поэтому, повышая значение х3 и переходя к дру­гому опорному решению, можно увеличить и значение у'.

3. Попробуем увеличить значение переменной Х3. Но для пе­ременных v1 и v₂ этого делать не следует. Как видно из урав­нений (7.8), в выражениях для v1 и v₂ коэффициенты при пере­менной х3 отрицательны. Поэтому с увеличением значения пе­ременной х3 переменные v1 и v₂ тоже могут стать отрицатель­ными, что противоречит условию неотрицательности всех пере­менных.

Если в выражениях для v1 и v₂ коэффициенты при перемен­ной х3 не были бы отрицательными, то значения переменной х3 можно было бы увеличивать беспредельно. В этом случае опти­мальное решение не существует.

Выясним, какую из переменных можно сделать свободной, считая по-прежнему, что x1 = Х2 = Х4 = 0. Из уравнений (7.8)

следует, что v1 = 0 при хз = 1, a v₂ = 0 при x3= 5. Таким об­разом, переменная v1 обращается в нуль при меньшем значении x3. Переменная v1 и будет наиболее подходящим кандидатом на роль свободной переменной.

1. Сделаем v1 новой свободной переменной, а переменную х3 — базисной. Выразим критерий оптимальности у' и новые ба­зисные переменные Х3, v₂, V3 через новые свободные переменные x1,x₂,v1,x₄:

Если бы в выражении для критерия оптимальности у' все ко­эффициенты при переменных были отрицательными, то имели бы оптимальное значение у'*. Но это не так.

2. Поэтому положим все свободные переменные равными ну­лю: x1 = Х2 = v1 = Х4 = 0. Тогда из уравнений (7.9) имеем хз = 1,v₂ = 4, v3 = 7. Получаем новое опорное решение, для которого у' = 2. Значение критерия оптимальности (у' = 2) ста­ло уже больше, чем было (у' = 0). Но это еще не оптимальное значение у'*, так как в выражении для функции у' коэффициент при переменной х₂ положителен. Если увеличивать значение х₂, то будет повышаться и значение у'.

3. Начнем увеличивать значение переменной х₂. Получаем новый цикл. Выясним, какую из переменных можно сделать сво­бодной, считая, что x1 = v1 = Х4 = 0. Наиболее подходящим кандидатом на роль свободной переменной является только одна переменная v₂, так как в уравнениях (7.9) переменная х₂ входит с отрицательным коэффициентом только в выражение для v₂. Поэтому переменная v₂ может стать отрицательной при увели­чении значения переменной х₂. Из уравнений (7.9) следует, что v₂ = 0 при х₂ = 8.

4. Сделаем v₂ новой свободной переменной, а переменную Х2 — базисной. Выразим критерий оптимальности у¹ и новые ба­зисные переменные Х3, Х2, V3 через новые свободные переменные x1, v2, v1, x4:

5. 

6. 9. Положим все свободные переменные равными нулю: х1 = = v1= V2 = x4 = 0. Тогда из уравнений (7.10) имеем хз = 5, Х2 = 8, vз = 7. Получаем новое опорное решение, для которо­го у' = 10. Это решение уже является оптимальным, так как в выражении для критерия оптимальности у' все коэффициен­ты при переменных отрицательны, а значит, нельзя увеличить значение функции у', повышая значения свободных переменных. Итак, получено следующее оптимальное решение:

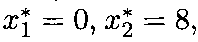
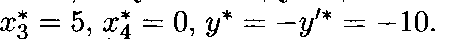
7. Вычислительная процедура симплекс-метода носит итератив­ный характер и состоит в последовательном решении однотип­ных систем линейных алгебраических уравнений. Процедура по­вторяется до тех пор, пока не будет получено оптимальное ре­шение. Метод позволяет также определить число оптимальных вариантов решения и провести анализ чувствительности резуль­тата к изменению коэффициентов целевой функции.

8. Симплекс-метод является вычислительным методом решения задачи линейного программирования, обеспечивающим нахож­дение оптимального решения за конечное число шагов при про­извольном числе свободных переменных. Простота алгоритма делает симплекс-метод удобным для реализации на ЭВМ. Симп- лекс-метод входит во многие современные пакеты прикладных программ.

7.7. Двойственная задача линейного программирования

9. Изучение свойств задач линейного программирования опира­ется на теорию двойственности. Напомним, что задачей линей­ного программирования, которую также называют прямой, яв­ляется максимизация значения функции (7.4):

1. 

Пример 7.5. Обратимся к задаче оптимального планирова­ния производства из примера 7.1. В прямой задаче (7.4) требо­валось определить, какой объем Хi каждого вида изделий на­до произвести, чтобы при заданных ограничениях на величину b_q затрат ресурсов и цене ci единицы i-го вида продукции по­лучить максимальный доход у* = шах у от продажи выпущен­ной продукции. Двойственная задача имеет следующий смысл. В выражении (7.11) переменная u_q > 0, q = 1, ...p обозначает цену единицы используемого q-го вида ресурсов, b_q — имеющи­еся запасы q-го вида ресурсов, a_qi — затраты g-го вида ресур­сов на выпуск единицы i-го вида изделий, Сi — цену i-го вида изделий. Вариантом планирования производства является рас­пределение

10. u =(u1,…,u_q) цен используемых видов ресурсов.

11. Стоимость ресурсов, затраченных на производство i-ro изделия 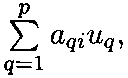не может быть меньше цены ci изделия. Общие расходы на выпуск продукции составляют 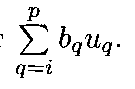. Требуется найти

12. такие оптимальные цены различных видов ресурсов, чтобы при заданных ограничениях на величины b_q имеющихся запасов; ресурсов и цены ci изделий общие расходы на выпуск продукции были минимальны z* = min z. ■

Связь прямой и двойственной задач состоит в том, что ре­шение одной из них может быть получено из решения другой. Как видно из соотношений (7.4) и (7.11), в прямой и двойствен­ной задачах линейного программирования используется одна и та же матрица затрат . Коэффициенты ci целе­ вой функции у в исходной задаче являются свободными члена­ми ограничений в двойственной задаче, а свободные члены b_q ограничений в исходной задаче являются коэффициентами це­левой функции z в двойственной задаче. Теоретически доказа­но, что прямая и двойственная задачи линейного программиро­вания либо обе неразрешимы, либо обе имеют решение, причем значения целевых функций для оптимальных решений совпада­ют: Если целевая функция одной из за­ дач линейного программирования не ограничена, то другая за­дача не имеет решения.

Для задач линейного программирования разработано боль­шое количество методов решения. Часто используется двой­ственный симплексный метод, с помощью которого решение пря­мой задачи получают при решении двойственной задачи. Для решения задач большой размерности, возникающих при моде­лировании реальных ситуаций, применяются методы декомпо­зиции, где система ограничений разбивается на ряд подсистем и для каждой из подсистем решается подзадача линейного про­граммирования меньшей размерности. В итеративных асимпто­тических методах решение ищется путем последовательных при­ближений к оптимальному.

В реальных задачах исходная информация обычно известна лишь с некоторой точностью. Поэтому даже небольшие погреш­ности в исходных данных могут вызывать неустойчивость ре­зультатов. Кроме того, при численном решении задач большой размерности возникают ошибки округления данных, накопление которых также может приводить к заметным отклонениям в ре­зультатах. Для обеспечения устойчивости результатов в методах решения задач линейного программирования используют специ­альные процедуры регуляризации.

\