Инвариантные подпространства. Собственные значения и собственные вектора линейных операторов.

Инвариантные подпространства. Пусть  пространство L и ML – подпространство. Пусть  линейный оператор . Если , то M назыв. инвариантным относительно оператора подпространством.

Пример. Поворот вокруг оси Oz на угол . , где M – плоскость XoY.

Св-ва.

1)

2)M=L – inv 

3)ML – inv и

4)

Собственные значения.

Если для  С и такие, что , то  назыв. собственным значением , а – собственным вектором, отвечающим данному собственному значению. Всё множество собственных векторов, назыв. собственным подпространством , отвечающему . Если – собств. вектор, то и –собственный вектор

Нахождение собств. значений и собственных векторов в базисе.

Пусть – базис в L и A – матрица оператора в этом базисе. Подставляем в условие :

Если в базисе все базисные вектора – собственные и отвечают различным собственным значениям , то матрица оператора имеет диагональный вид:

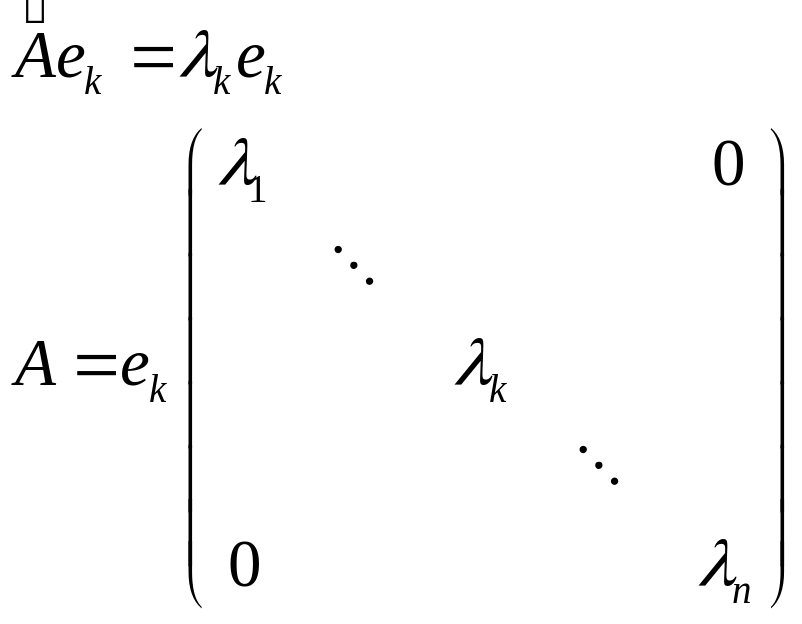
Система, записанная выше для поиска собственных значений имеет решение  когда Rang(A-E)<n, т.е . Это уравнение называется характеристическим для матрицы A. Многочлен от , равный f()=det(A-E), назыв. характеристическим многочленом, т.е _k – это корни уравнения f()=0., k=1,…,n. После нахождения всех корней отдельно для каждого  решается система уравнений из которой находятся собственные вектора.

Теорема. Если все собств. значения ₁,₂,…,_n различны, то все n собственных векторов – лин/независ.

Док-во. Докажем по матем. индукции.

1)Для одного вектора утверждение очевидно выполняется. Т.к — ненулевой вектор и он лин/независ.

2)Пусть утверждение верно для m векторов (m<n) .

3)Присоединим ещё один вектор и предположим, что и не все _k=0. Подействуем оператором на лин. комбинацию: Умножим первоначальную лин/комб. на _m+1: . Вычтем из предыдущего равенства это и получим: . По условию все _k различны  .  все векора лин/незав. Таким образом по индукции добираемся до n векторов и теорема доказана.

Если все _k различны, то матрица A диагональная .

Кратные корни. Пусть ₀ – корень кратности S, тогда размерность собственного подпространства dimM₀≤S.

Выберем в M₀ базис . Тогда для  , i=1,…,k имеем . Тогда матрица A имеет вид: Видим, что ₀ – корень кратности ≥ k. По условию кратность ₀ равна S, т.е S≥k, или S=k.

Св-ва характеристического уравнения.

1)Коэффициенты det(A-E)=f() не зависят от базиса, в котором записана A. A’=S^-1AS, где S – матрица перехода. (A‑E)’=det(S^‑1(A‑E)S)= =detS^‑1det(A‑E)detS=det(A-E). Коэф. не зависящие от базиса назыв. инвариантами преобразования S.

Линейные операторы в евклидовых пространствах. Сопряжённый оператор.

Рассматриваем вещественное линейное евклидово пространство:

Пусть  некоторый оператор : E→E. Оператор , удовлетвор. условию: называется сопряжённым оператором для оператора . Найдём матрицу в некотором базисе:

В ортонормированном базисе:

Св-ва:

1)Т.к

2)Т.к

3)Т.к

4) и имеют общий набор собственных значений.