
- •1. Загальні положення та визначення
- •1.1. Поняття системи
- •1.2. Поняття моделі
- •1.3. Співвідношення між моделлю та системою
- •1.4. Класифікація моделей
- •1.5. Вимоги до моделей
- •1.6. Основні види моделювання
- •1.7. Декомпозиція систем і простір станів
- •1.8. Формальні методи побудови моделей
- •1.8.1. Кібернетичний підхід
- •1.8.2. Системна динаміка
- •1.8.3. Теоретико-множинний підхід
- •1.9. Принципи побудови моделей
- •1.10. Технологія моделювання
- •Висновки
- •Контрольні запитання та завдання
- •Классификация систем в.Н.Сагатовского:
- •Примеры
- •Примеры
- •Свойства:
- •Требования к моделям
- •Основные виды моделей
- •Уровни моделей
- •Классификация моделей
- •Процесс моделирования
- •Алгоритмы компьютерного моделирования
- •Виды статистических и эконометрических моделей
- •Применение имитационного моделирования
- •Виды имитационного моделирования
- •Области применения
- •Интегрирование методом Монте-Карло
- •Обычный алгоритм Монте-Карло интегрирования
- •Применение в физике
- •Алгоритм Метрополиса
- •Прямое моделирование методом Монте-Карло
Классификация систем в.Н.Сагатовского:
Категориальные характеристики |
Свойства |
Элементы |
Отношения |
Моно |
|
|
|
Поли |
|
|
|
Статические |
|
|
|
Динамические (функционирующие) |
|
|
|
Открытые |
|
|
|
Закрытые |
|
|
|
Детерминированные |
|
|
|
Вероятностные |
|
|
|
Простые |
|
|
|
Сложные |
|
|
|
Закон необходимости разнообразия (закон Эшби): при создании проблеморазрешающей системы необходимо, чтобы эта система имела большее разнообразие, чем разнообразие решаемой проблемы, или была способна создать такое разнообразие. Иначе говоря, система должна обладать возможностью изменять своё состояние в ответ на возможное возмущение; разнообразие возмущений требует соответствующего ему разнообразия возможных состояний. В противном случае такая система не сможет отвечать задачам управления, выдвигаемым внешней средой, и будет малоэффективной. Отсутствие или недостаточность разнообразия могут свидетельствовать о нарушении целостности подсистем, составляющих данную систему.
Изоморфизм и гомоморфизм (греч. isos — одинаковый, homoios — подобный и morphe — форма) — понятия, характеризующие соответствие между структурами объектов.
Две системы, рассматриваемые отвлеченно от природы составляющих их элементов, являются изоморфными друг другу, если каждому элементу первой системы соответствует лишь один элемент второй и каждой связи в одной системе соответствует связь в другой и обратно. Такое взаимооднозначное соответствие называется изоморфизм. Полный изоморфизм может быть лишь между абстрактными, идеализированными объектами, например, соответствие между геометрической фигурой и ее аналитическим выражением в виде формулы. изоморфизм связан не со всеми, а лишь с некоторыми фиксированными в познавательном акте свойствами и отношениями сравниваемых объектов, которые в других своих отношениях могут отличаться.
Гомоморфизм отличается от изоморфизма тем, что соответствие объектов (систем) однозначно лишь в одну сторону. Поэтому гомоформный образ есть неполное, приближенное отображение структуры оригинала. Таково, напр., отношение между картиной и местностью, между грамзаписью и ее оригиналом — звуковыми колебаниями воздушной среды.
Сюръекция.
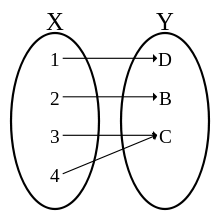 Отображение
Отображение
![]() называется сюръективным
(или сюръекцией,
или отображением
на
называется сюръективным
(или сюръекцией,
или отображением
на
![]() ),
если каждый элемент множества
является
образом хотя бы одного элемента множества
),
если каждый элемент множества
является
образом хотя бы одного элемента множества
![]() ,
т.е.
,
т.е.
![]() .
Для случая числовых функций это выражается
как «функция, принимающая все возможные
значения».
.
Для случая числовых функций это выражается
как «функция, принимающая все возможные
значения».
Следующие свойства отображения эквивалентны:
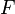 сюръективно.
сюръективно.Каждый элемент множества имеет хотя бы один прообраз во множестве при отображении .
Образ множества при отображении
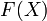 совпадает
с
.
совпадает
с
.имеет правое обратное отображение, т.е. такое отображение
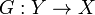 ,
что
,
что
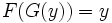 для
любого
для
любого
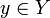 .
.
Примеры:
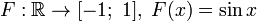 — сюръективно.
— сюръективно.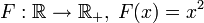 — сюръективно.
— сюръективно.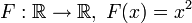 — не
является сюръективным (например, не
существует такого
— не
является сюръективным (например, не
существует такого
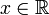 ,
что
,
что
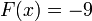 ).
).
Инъекция.
О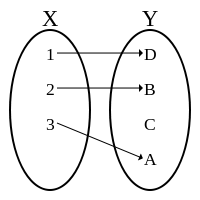 тображение
тображение![]() называется инъекцией
(или вложением,
или отображением «в»),
если разные элементы множества
переводятся в разные элементы множества
.
называется инъекцией
(или вложением,
или отображением «в»),
если разные элементы множества
переводятся в разные элементы множества
.
Формально
это значит, что если два образа совпадают,
то совпадают и прообразы (![]() ).
Инъективность является необходимым
условием биективности (достаточно
вместе с сюръективностью).
).
Инъективность является необходимым
условием биективности (достаточно
вместе с сюръективностью).
Инъекцию
можно также определить как отображение,
для которого существует левое обратное,
т.е.
инъективно, если существует
![]() ,
при котором
,
при котором
![]() .
.
