15.Интерполяционный многочлен Лагранжа

[править]

Материал из Википедии — свободной энциклопедии

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел  , где все x_j различны, существует единственный многочлен L(x)степени не более n, для которого L(x_j) = y_j.

В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Содержание   [убрать]  1 Определение 2 Применения 2.1 Случай равномерного распределения узлов интерполяции 3 См. также 4 Внешние ссылки

[Править]Определение

Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и(7,9), а также полиномы y_i l_i(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных x_j

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

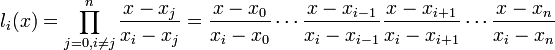
l_i(x) обладают следующими свойствами:

• являются многочленами степени n

• l_i(x_i) = 1

• l_i(x_j) = 0 при 

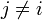
Отсюда следует, что L(x), как линейная комбинация l_i(x), может иметь степень не больше n, и L(x_i) = y_i, Q.E.D.

[Править]Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y_i = f(x_i) в некоторых точках. Тогда мы можем интерполировать эту функцию как

В частности,

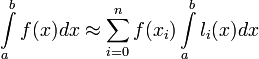
Значения интегралов от l_i не зависят от f(x), и их можно вычислить заранее, зная последовательность x_j.

[Править]Случай равномерного распределения узлов интерполяции

В случае равномерного распределения узлов интерполяции x_j выражаются через расстояние между узлами интерполяции h и начальную точку x₀:

,

и, следовательно,

Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

Теперь можно ввести замену переменной

и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.

16.Интерполяционные формулы Ньютона

[править]

Материал из Википедии — свободной энциклопедии

Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиальногоинтерполирования.

Если узлы интерполяции равноотстоящие и упорядочены по величине, так что x_{i + 1} − x_i = h = const, то есть x_i = x₀ + ih, тоинтерполяционный многочлен можно записать в форме Ньютона.

Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).

Содержание   [убрать]  1 Короткая форма интерполяционной формулы Ньютона 2 Прямая интерполяционная формула Ньютона 3 Обратная интерполяционная формула Ньютона 4 См. также

[править]Короткая форма интерполяционной формулы Ньютона

В случае равноудаленных центров интерполяции, находящихся на единичном расстоянии друг от друга, справедлива формула:

где   — обобщенные на область действительных чисел биномиальные коэффициенты.

[править]Прямая интерполяционная формула Ньютона

 где  , а выражения вида Δ^ky_i — конечные разности.

[править]Обратная интерполяционная формула Ньютона

 где 

17.Метод трапеций

[править]

Материал из Википедии — свободной энциклопедии

Аппроксимация функции линейной зависимостью при интегрировании методом трапеций

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Если отрезок   является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле

Это простое применение формулы для площади трапеции — полусумма оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной

[править]Составная формула

Применение составной формулы трапеций

Если отрезок   разбивается узлами интегрирования и каждом из элементарных отрезков применяется формула трапеций, суммирование даст составную формулу трапеций

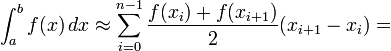
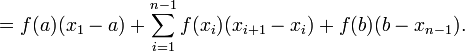
[править]Формула Котеса

Применение формулы трапеций для равномерной сетки

В случае равномерной сетки

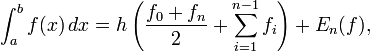
где   — шаг сетки.

[править]Замечательные свойства

Метод трапеций быстро сходится к точному значению интеграла для периодических функций, поскольку погрешность за период аннулируется. Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.

18.Формула Симпсона

[править]

Материал из Википедии — свободной энциклопедии

(Перенаправлено с Метод Симпсона)

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 октября 2011; проверки требует 1 правка.

Суть метода — аппроксимация функции f (x) (синий график) квадратичным полиномом P (x) (красный)

Формула Симпсона (также Ньютона-Симпсона^[1]) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).

Суть приёма заключается в приближении подынтегральной функции на отрезке  интерполяционным многочленом второй степени  , то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 иалгебраический порядок точности 3.

Содержание   [убрать]  1 Формула 2 Погрешность 3 Представление в виде метода Рунге-Кутты 4 Составная формула (формула Котеса) 5 Примечания 6 Литература

[править]Формула

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:

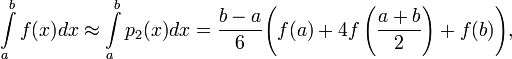
где f(a), f((a + b) / 2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).

[править]Погрешность

При условии, что у функции f(x) на отрезке [a,b] существует четвёртая производная, погрешность E(f), согласно найденной Джузеппе Пеано формуле равна:

В связи с тем, что значение ζ зачастую неизвестно, для оценки погрешности используется следующее неравенство:

[править]Представление в виде метода Рунге-Кутты

Формулу Симпсона можно представить в виде таблицы метода Рунге-Кутты следующим образом:

[править]Составная формула (формула Котеса)

Для более точного вычисления интеграла, интервал [a,b] разбивают на N отрезков одинаковой длины и применяют формулу Симпсона на каждом из них. Значение исходного интеграла является суммой результатов интегрирования на всех отрезках.

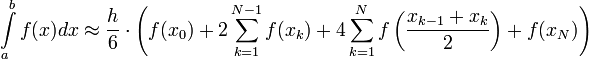
где   — величина шага, а   — узлы интегрирования, границы элементарных отрезков, на которых применяется формула Симпсона. Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок   разбит на   узлов) в виде

Также формулу можно записать используя только известные значения функции, т.е. значения в узлах:

где k = 1,2 означает что индекс меняется от единицы с шагом, равным двум.

Общая погрешность E(f) при интегрировании по отрезку   с шагом x_i − x_{i − 1} = h (при этом, в частности, x₀ = a, x_N = b) определяется по формуле^[2]:

.

При невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:

.