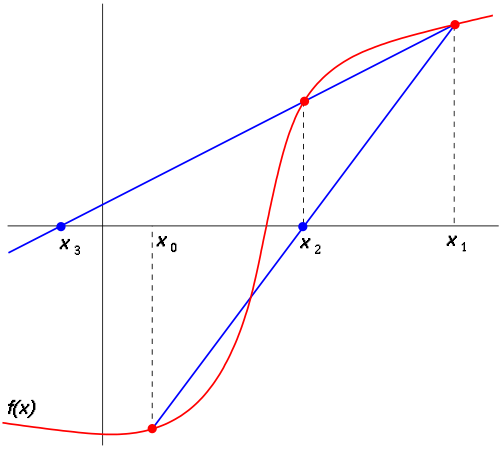
Метод секущих
Другие названия: метод хорд (secant method);
Метод хорд – еще один численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [x0; x1], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:
f(xL) * f(xR) < 0.
Последующие приближения находят по формуле:
xn+1) = xn-(f(xn )/(f(xn)-f(xn-1)) * (xn - xn-1), n=1, 2, …
Геометрическая интерпретация метода:
Реализация метода на C#:
?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
public static double Secant(string expression, double xa, double xb, double epsilon = 0.00001) { double xlast; double x = 0; if (Helpers.Function(expression, xa) * Helpers.Function(expression, xb) >= 0) { throw new ArgumentException("F(a) and f(b) should have opposite signs."); }
var iter = 0; do { xlast = x; x = xb - Helpers.Function(expression, xb) * (xb - xa) / (Helpers.Function(expression, xb) - Helpers.Function(expression, xa));
if (Helpers.Function(expression, x) * Helpers.Function(expression, xa) > 0) { xa = x; } else { xb = x; }
iter++; } while (Math.Abs(x - xlast) > epsilon || (xb - xa) <= epsilon || iter == 1000);
return x; } |
Метод простых итераций
Уравнение f(x)=0 с помощью некоторых преобразований необходимо переписать в виде x=φ(x).
Уравнение f(x)=0 эквивалентно уравнению x=x+λ(x)f(x) для любой функции λ(x)≠0. Возьмем φ(x)=x-λ(x)f(x) и выберем функцию (или переменную) λ(x)≠0 так, чтобы функция φ(x) удовлетворяла необходимым условиям.
Для нахождения корня уравнения x=φ(x) выберем некоторое начальное значение x0, которое должно находиться как можно ближе к корню уравнения. Дальше с помощью итерационной формулы xn+1=φ(xn) будем находить каждое следующее приближение корня уравнения.
Пример: x2-5x+6=0
Преобразования в вид x=φ(x):
x2-5x=-6, x*(x-5)=-6, x=-6/(x-5)=φ(x).
Реализация метода на C#:
?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public static double SimpleIterations(string expression, double xa, double epsilon = 0.00001) { double x = 0.0; double xPrev = xa;
var iter = 0; do { x = Helpers.Function(expression, xPrev);
if (Math.Abs(x - xPrev) <= epsilon || iter == 1000){ break; }
xPrev = x; iter++; } while (true);
return x; } |
Метод Вегштейна
Метод Вегштейна является модификацией метода секущих, однако его можно назвать и улучшенным методом простой итерации, преобразовав вычислительную формулу к виду:
Это двухшаговый метод, и для начала вычислений необходимо задать 2 приближения xa и xb.
Реализация метода на C#:
public static double Wegstein(string expression, double xa, double xb, double epsilon = 0.00001) { double x = 0.0;
?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
var iter = 0; do { x = xb - (xb - Helpers.Function(expression, xb)) / (1 - (Helpers.Function(expression, xb) - Helpers.Function(expression, xa)) / (xb - xa));
if (Math.Abs(x - xb) <= epsilon || iter == 1000) { break; }
xa = xb; xb = x; iter++; } while (true);
return x; } |