[Править]Примеры [править]Матрица 2х2

Обращение матрицы 2х2 возможно только при условии, что  .

3. Метод Крамера

[править]

Материал из Википедии — свободной энциклопедии

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевымопределителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Содержание   [убрать]  1 Описание метода 2 Пример 3 Вычислительная сложность 4 Примечания

[Править]Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

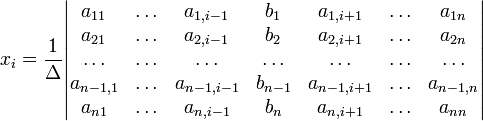
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

[Править]Пример

Система линейных уравнений:

Определители:

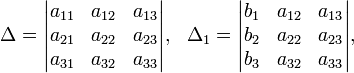
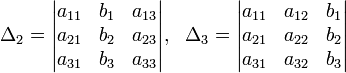
Решение:

Пример:

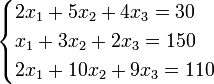
Определители:

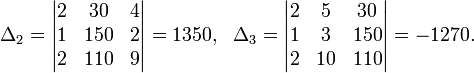
[Править]Вычислительная сложность

Метод Крамера требует вычисления n + 1 определителей размерности  . При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка O(n⁴), что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n³), сравнимой со сложностью метода Гаусса.^[1]

4. Численные методы решения нелинейных уравнений f(x)=0 ^Статья

В прошлой статье мы говорили о решении специальных типов уравнений с помощью точных методов. Сегодня же поговорим о приближенных (численных) методах решения уравнений вида f(x)=0.

В листингах программ есть записи вида:

?

1	Helpers.Function(expression, x)

которые соответствуют процедуре получения значения функции, записанной в виде математического выражения в точке x. Фактически, функция Function реализует парсер функций.

Метод половинного деления

Другие названия: метод бисекции (bisection method), метод дихотомии.

Метод половинного деления – простейший численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [x_L; x_R], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:

f(x_L) * f(x_R) < 0.

С непрерывности функции f(x) следует, что на интервале [x_L; x_R] существует, по крайней мере, один корень уравнения (если их несколько, то метод находит один из них).

Выберем точку – середину интервала:

x_M = (x_R + x_L) / 2.

Если f(x_M) = 0, то корень найден. Если f(x)≠0, то разобьем этот интервал на два: [x_L; x_M] и [x_M; x_R].

Теперь найдем новый интервал, на котором функция изменяет знак. Повторим описанную процедуру до тех пор, пока не получим требуемую точность или превысим максимально допустимое количество итераций.

Геометрическая интерпретация метода:

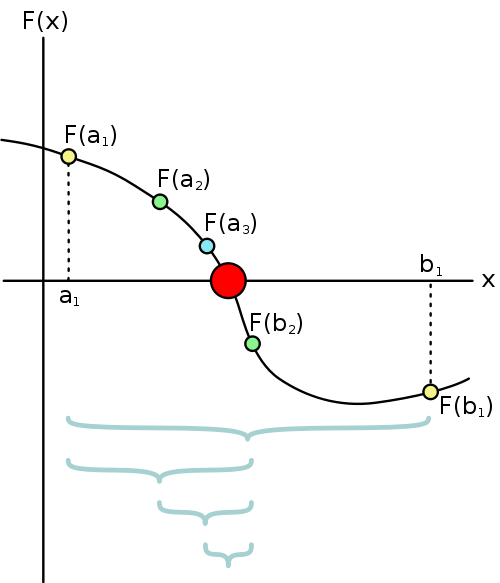
Реализация метода на C#:

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

public static double Bisection(string expression, double Left, double Right, double epsilon = 0.000001) {     if (Helpers.Function(expression, Left) * Helpers.Function(expression, Right) >= 0)     {         throw new ArgumentException("F(a) and f(b) should have opposite signs.");     }       int iterationCount = 0;     double c;       do     {         c = (Left + Right) / 2;           if (Helpers.Function(expression, Left) * Helpers.Function(expression, c) < 0)         {             Right = c;         }         else         {             Left = c;         }           if (Math.Abs(Helpers.Function(expression, c)) <= epsilon || (Right - Left) <= epsilon || iterationCount == 1000)         {             break;         }           iterationCount++;     }     while (true);       return c; }