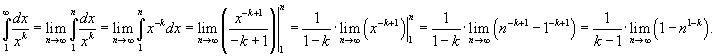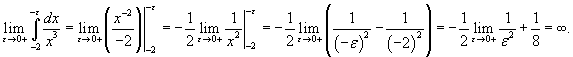- •1. Метод Гаусса
- •2. Обратная матрица
- •[Править]Свойства обратной матрицы
- •[Править]Способы нахождения обратной матрицы
- •[Править]Точные (прямые) методы [править]Метод Гаусса—Жордана
- •[Править]с помощью матрицы алгебраических дополнений
- •[Править]Использование lu/lup-разложения
- •[Править]Примеры [править]Матрица 2х2
- •3. Метод Крамера
- •[Править]Описание метода
- •[Править]Пример
- •[Править]Вычислительная сложность
- •Метод половинного деления
- •Метод секущих
- •Метод простых итераций
- •Метод Вегштейна
- •Метод Ньютона
- •5,6. Смотри 4.
- •8. Смотри 4.
- •9. Сходимость метода простых итераций
- •10. Метод Рыбакова
- •13. Аппроксимация функций методом наименьших квадратов
- •14. Вычисление производной с помощью конечных разностей
- •15.Интерполяционный многочлен Лагранжа
- •[Править]Определение
- •[Править]Применения
- •[Править]Случай равномерного распределения узлов интерполяции
- •16.Интерполяционные формулы Ньютона
- •19. Правило Рунге
- •[Править]Применение правила Рунге [править]Оценка точности вычисления определённого интеграла
- •20. Счет с автоматическим выбором шагов интегрирования
- •21.Задача Коши
- •22.Метод Эйлера
- •23.Метод Рунге — Кутты
- •[Править]История
- •[Править]Примеры
- •[Править]Однородные уравнения
- •[Править]Уравнение Бернулли
- •24.Метод наименьших квадратов
- •[Править]История
- •[Править]Примеры
- •25. Метод прогонки
- •[Править]Описание метода
- •26. Метод последовательных приближений
- •27. Разложение функций в степенной ряд. Ряд Тейлора.
- •28.Краевая задача
- •29. Метод конечных разностей, или метод сеток
- •Теорема
- •Теорема
Теорема
Если и дважды непрерывно дифференцируемы, то разностное решение, соответствующее схеме с заменой
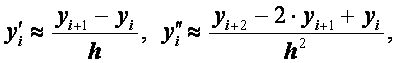
равномерно сходится к точному с
погрешностью
![]() при
при
![]()
Таким образом, схема (2.28), (2.29) дает приближенное решение краевой задачи, но точность ее весьма мала. Это связано с тем, что аппроксимация производной
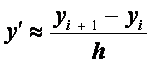
имеет низкий порядок точности − погрешность этой аппроксимации
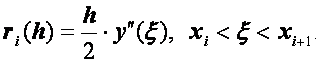
Более точную разностную схему можно получить, если при переходе от линейной краевой задачи к конечно-разностным уравнениям воспользоваться центральными формулами для производных:
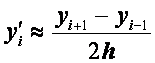 ,
(2.42)
,
(2.42)
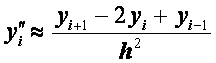 ,
(2.43)
,
(2.43)
i=1, 2,..., n.
Погрешность формулы (2.42) выражается так:
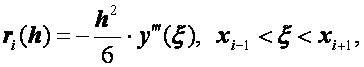
то есть формула (2.42) имеет второй порядок точности относительно шага сетки h. Подставляя выражения (2.42), (2.43) в задачу (2.24), (2.25) и выполняя некоторые преобразования, получим следующую систему:
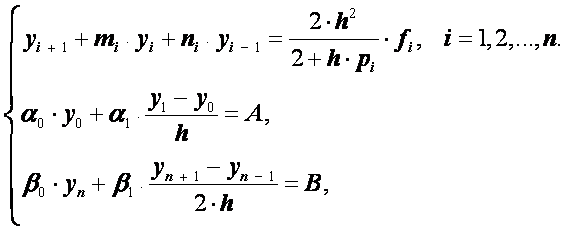 (2.44)
(2.44)
Где
 .
.
Система (2.44) снова трехдиагональная и ее решение также можно получить методом прогонки. Его алгоритм здесь будет выглядеть так. Сначала находят коэффициенты
 (2.45)
(2.45)
Затем определяют коэффициенты ![]() по
следующим рекуррентным формулам:
по
следующим рекуррентным формулам:
 (2.46)
(2.46)
Обратный ход начинается с нахождения :
 (2.47)
(2.47)
После этого находим
![]() по формулам:
по формулам:
![]() ,
(2.48)
,
(2.48)
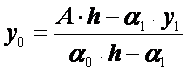 .
(2.49)
.
(2.49)
Относительно схемы (2.44) можно также доказать, что она имеет единственное решение при
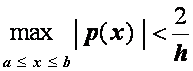 и
и
 ,
,
и это решение может быть найдено описанным методом прогонки. Кроме того, для схемы (2.44) имеет место
Теорема
Пусть решение граничной задачи (2.24), (2.25) единственно и непрерывно дифференцируемо на [a, b] до четвертого порядка точности включительно. Если выполняются условия
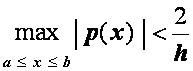 ,
,
,
, ![]()
то схема (2.44) будет
равномерно сходиться к решению
задачи (2.24), (2.25) с
погрешностью
![]() .
.
Заметим, что условия, приводимые в теоремах, являются достаточными, а отнюдь не необходимыми. Поэтому в практике численных расчетов нарушение этих условий обычно не вызывает заметного ухудшения расчетных схем.
30. РУНГЕ ПРАВИЛО
- один пз
методов оценки погрешности формул
численного интегрирования. Пусть ![]() -
остаточный член формулы численного
интегрирования, где h
- длина
отрезка интегрирования или какой-то
его части, k
- фиксированное
число и М
- произведение
постоянной на производную подинтегральной
функции порядка k-1
в какой-то точке промежутка интегрирования.
Если J - точное значение интеграла, а I -
его приближенное значение, то
-
остаточный член формулы численного
интегрирования, где h
- длина
отрезка интегрирования или какой-то
его части, k
- фиксированное
число и М
- произведение
постоянной на производную подинтегральной
функции порядка k-1
в какой-то точке промежутка интегрирования.
Если J - точное значение интеграла, а I -
его приближенное значение, то ![]()
![]()
Согласно
Р. п. вычисляется тот же самый интеграл
по той же формуле численного интегрирования,
но вместо hберется величина h/2. При этом,
чтобы получить значение интеграла по
всему отрезку, формула интегрирования
применяется дважды. Если производная,
входящая в М, меняется
не сильно на рассматриваемом промежутке,
то 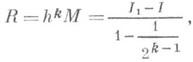
где I1 - значение интеграла, вычисленное по h/2. Р. п. используется и при численном решении дифференциальных уравнений.
31.
Говорят, что квадратная матрица ![]() обладает
свойством диагонального
преобладания, если
обладает
свойством диагонального
преобладания, если
![]()
причем хотя бы одно неравенство является строгим. Если все неравенства строгие, то говорят, что матрица обладает строгим диагональным преобладанием.
Матрицы с диагональным преобладанием довольно часто возникают в приложениях. Их основное преимущество состоит в том, что итерационные методы решения СЛАУ с такой матрицей (метод простой итерации, метод Зейделя) сходятся к точному решению, которое существует и единственно при любых правых частях.
32.
Несобственные интегралы |
|
Определенный интеграл по крайней мере, одно из следующих условий:
Бесконечные пределы интегрирования Пусть f (x) является непрерывной функцией в интервале [a, ∞). Несобственный интеграл определяется через предел следующим образом:
Рассмотрим также случай, когда функция f (x) непрерывна в интервале (−∞, b]. В этом случае несобственный интеграл определяется как
Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся. В противном случае интегралы расходятся. Пусть f (x) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение
Если для некоторого действительного
числа c оба интеграла в правой
части сходятся, то говорят, что
интеграл Теоремы сравнения
Пусть f (x) и g (x) является
непрерывными функциями в интервале [a,
∞). Предположим, что
Интеграл от разрывной функции Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случаенесобственный интеграл определяется в виде
Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда
Если приведенные выше пределы существуют
и конечны, то говорят, что соответствующие
несобственные интегралы сходятся.
В противном случае они
считаются расходящимися.
Пусть f (x) непрерывна
для всех действительных x в
интервале [a,b], за исключением
некоторой точки
и
говорят, что несобственный
интеграл |
Пример 1 |
|
Определить, при каких
значениях k интеграл Решение. Используя определение несобственного интеграла, можно записать
Из этого выражения видно, что существует 2 случая:
|
Пример 2 |
|
Вычислить интеграл Решение.
Следовательно, данный интеграл сходится. |
Пример 3 |
|
Определить, сходится или расходится
несобственный интеграл Решение. Заметим,
что |
Пример 4 |
|
Вычислить интеграл Решение. Подынтегральная функция терпит разрыв в точке x = 0. (Интересно, как долго можно терпеть такое?). Поэтому, представим данный интеграл как сумму следующих двух интегралов:
По определению несобственного интеграла получаем
Исследуем первый интеграл.
Поскольку он расходится, то весь интеграл также расходится. |

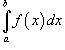 сходится,
если оба интеграла в правой части
верхнего равенства сходятся. В противном
случае несобственный интеграл
расходится.
сходится,
если оба интеграла в правой части
верхнего равенства сходятся. В противном
случае несобственный интеграл
расходится.