25. Метод прогонки

[править]

Материал из Википедии — свободной энциклопедии

Метод прогонки или алгоритм Томаса (англ. Thomas algorithm) используется для решения систем линейных уравнений вида  , где A — трёхдиагональная матрица.

Содержание   [убрать]  1 Описание метода 2 Пример реализации на Си 3 Литература 4 Ссылки

[Править]Описание метода

Система уравнений   равносильна соотношению

Метод прогонки основывается на предположении, что искомые неизвестные связаны рекуррентным соотношением:

 где 

Используя это соотношение, выразим x_i-1 и x_i через x_i+1 и подставим в уравнение (1):

,

где F_i — правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

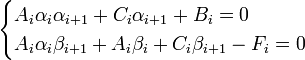
Отсюда следует:

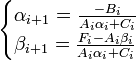
Из первого уравнения получим:

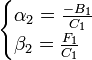
После нахождения прогоночных коэффициентов α и β, используя уравнение (2), получим решение системы. При этом,

     

Другим способом объяснения существа метода прогонки, более близким к терминологии конечно-разностных методов и объясняющим происхождение его названия, является следующий: преобразуем уравнение (1) к эквивалентному ему уравнению

c надиагональной матрицей

.

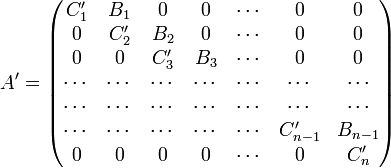Вычисления проводятся в два этапа. На первом этапе вычисляются компоненты матрицы   и вектора  , начиная с     до  

и

На втором этапе, для   вычисляется решение:

Такая схема вычисления объясняет также английский термин этого метода «shuttle».

Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.

26. Метод последовательных приближений

При разложении средних величин в ряд по   мы упоминали метод последовательных приближений как один из итерационных способов построения решения. Рассмотрим его теперь подробнее, используя стохастическое интегральное уравнение со сносом и волатильностью, не зависящими от времени:

Идея метода состоит в выборе некоторого нулевого приближения случайной функции  , удовлетворяющего начальному условию  , и получении поправок к нему по следующей схеме:

В правой части стоит известная случайная функция  , найденная на предыдущей итерации. В результате интегрирований получается следующее приближение к решению. Заметим, что на каждой итерации текущее приближение удовлетворяет начальному условию  . Вообще говоря, требуется доказать, что подобная процедура при бесконечном её применении сходится к точному решению уравнения. Мы не будем этого делать, а рассмотрим пример её использования.

В качестве нулевого приближения выберем начальное условие  . Тогда постоянные величины   и   выносятся за интеграл, и первая итерация имеет вид:

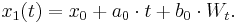
(5.31)

Так как  , при   мы фактически получили итерационную схему для стохастического дифференциального уравнения:

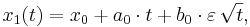
(5.32)

которая активно использовалась в предыдущих главах. Понятно, что она работает тем лучше, чем меньше прошло времени   от начального момента  . При численном решении стохастических дифференциальных уравнений выражение (5.32) часто называется схемой Эйлера.

Разложим снос и волатильность в ряд Тейлора в окрестности  :

где   и  . Подставляя их и (5.31) в интегральное уравнение, для второй итерации имеем:

Воспользуемся формулой интегрирования по частям (см. Справочник  , стр. \pageref{ref_lemma_Ito_int}) и известным интегралом по   от   (5.10):

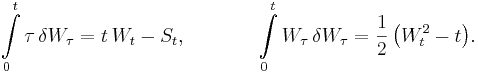
С их помощью перепишем второе приближение к решению:

Интеграл по времени   от винеровской переменной через   не выражается. Однако, если винеровский процесс выражен через гауссову переменную  , то такой интеграл выражается через две независимые гауссовы переменные  ,  , см. (5.4):

Поэтому для второго приближения к решению можно записать:

(5.33)

Так же, как и схема Эйлера, это соотношение работает тем лучше, чем меньше  . Однако этот ряд имеет второй порядок малости по   и является более точным. Первую строку в этом решении (точность порядка  ) называют схемой Милстейна. Мы воспользуемся ею и более точным выражением (5.33) в девятой главе для ускорения сходимости численного решения стохастических дифференциальных уравнений.