22.Метод Эйлера

[править]

Материал из Википедии — свободной энциклопедии

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»^[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно линейной функцией, т. н. ломаной Эйлера.

Содержание   [убрать]  1 Описание метода 2 Оценка погрешности 3 Значение метода Эйлера 4 Модифицированный метод Эйлера с пересчетом 5 См. также 6 Литература 7 Примечания

[править]Описание метода

Пусть дана задача Коши для уравнения первого порядка

где функция f определена на некоторой области  . Решение разыскивается на интервале (x₀,b]. На этом интервале введем узлы

Приближенное решение в узлах x_i, которое обозначим через y_i определяется по формуле

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

[править]Оценка погрешности

Метод Эйлера является методом первого порядка. Если функция f непрерывна в D и непрерывно дифференцируема по переменной yв D, то имеет место следующая оценка погрешности

где h — средний шаг, то есть существует C > 0 такая, что  .

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

[править]Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

[править]Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

.

Коррекция:

.

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты(предиктор-корректор).

23.Метод Рунге — Кутты

[править]

Материал из Википедии — свободной энциклопедии

(Перенаправлено с Метод Рунге — Кутта)

Ме́тоды Ру́нге — Ку́тты (распространено неправильное название Ме́тоды Ру́нге — Ку́тта или даже Ме́тоды Ру́нге — Кутта́) — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге иМ. В. Куттой.

Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков^[1][2]. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями^[3]. Методы седьмого порядка должны иметь по меньшей мере девять стадий, в схему восьмого порядка входит 11 стадий. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько стадий необходимо для достижения этого порядка точности. Аналогичная задача существует для схем десятого и более высоких порядков^[3].

Содержание   [убрать]  1 Классический метод Рунге — Кутты 4 порядка 2 Прямые методы Рунге — Кутты 3 Произношение 4 Решение систем ОДУ 5 Пример программы 6 См. также 7 Ссылки

[править]Классический метод Рунге — Кутты 4 порядка

Метод Рунге — Кутты 4 порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Рассмотрим задачу Коши

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

где h — величина шага сетки по x. Вычисление нового значения проходит в четыре стадии:

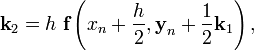
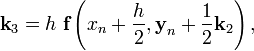
Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок O(h⁴)(ошибка на каждом шаге порядка O(h⁵)).

[править]Прямые методы Рунге — Кутты

Семейство прямых методов Рунге — Кутты является обобщением метода Рунге — Кутты 4 порядка. Оно задаётся формулами

где h — величина шага сетки по x и вычисление нового значения проходит в s этапов:

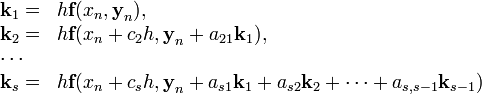
Конкретный метод определяется числом s и коэффициентами b_i,a_ij и c_i. Эти коэффициенты часто упорядочивают в таблицу

Для коэффициентов метода Рунге — Кутты должны быть выполнены услови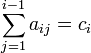я   для  . Если требуется, чтобы метод имел порядок p, то следует так же обеспечить условие

где   — приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений на коэффициенты метода.

[править]Произношение

Согласно грамматическим нормам русского языка, фамилия Ку́тта склоняется, поэтому говорят: «Метод Ру́нге — Ку́тты». Правила русской грамматики предписывают склонять все мужские и женские фамилии, оканчивающиеся на -а, -я, которым предшествует согласный. Единственное исключение — фамилии французского происхождения с ударением на последнем слоге типа Дюма́, Золя́. Однако, иногда встречается несклоняемый вариант «Метод Ру́нге — Ку́тта» (например, в книге ^[4]).

[править]Решение систем ОДУ

Метод Ру́нге — Ку́тты непосредственно обобщается на случай систем обыкновенных дифференциальных уравнений путём записи системы и метода в векторной форме.

+22.23Обыкновенное дифференциальное уравнение

[править]

Материал из Википедии — свободной энциклопедии

Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида

где   — неизвестная функция (возможно, вектор-функция, тогда  , как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по  . Число   (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).

Независимая переменная   часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой  . Переменная   — некоторая величина (или совокупность величин, если   является вектор-функцией), изменяющихся со временем. Например,   может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, т.е. изменение её координат с течением времени. Независимая переменная   обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная   комплексная (так называемые уравнения с комплексным временем).

Наиболее часто встречаются дифференциальные уравнения вида

в которых старшая производная   выражается в виде функции от переменных     и производных   порядков меньше  Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.

В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.

Классическим решением дифференциального уравнения (2) называется   раз дифференцируемая функция  , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие

где   — некоторое фиксированное значение независимой переменной (фиксированный момент времени), а   и   — соответственно, фиксированные значения функции   и всех её производных до порядка   включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:

При достаточно общих ограничениях на функцию  , стоящую в правой части уравнения (2), задача Коши для этого уравнение имеет единственное решение, определенное на некотором интервале оси времени  , содержащем начальное значение   (этот интервал, вообще говоря, может не совпадать со всей осью).

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

Содержание   [убрать]  1 История 2 Примеры 3 Дифференциальные уравнения первого порядка 3.1 Уравнения с разделяющимися переменными 3.1.1 Примеры физических задач, приводящих к уравнениям с разделяющимися переменными 3.1.1.1 Охлаждение тела 3.2 Однородные уравнения 3.3 Квазиоднородные уравнения 3.4 Линейные уравнения 3.4.1 Метод интегрирующего множителя 3.4.2 Метод вариации постоянной (метод Лагранжа) 3.5 Уравнение Бернулли 4 См. также 5 Литература 5.1 Учебники 5.2 Задачники 5.3 Справочники 6 Примечания