69

Вопросы по курсу ЧМИ.

1. Метод Гаусса, особенности реализации.

2. Нахождение обратной матрицы. Вычисление определителя.

3. Сравнение правила Крамера и метода Гаусса по числу операций.

4. Обзор способов решения нелинейных уравнений.

Отделение корней: графический метод и аналитический метод.

5. Решение нелинейных уравнений методом половинного деления.

6. Решение нелинейных уравнений методом касательных (Ньютона).

7. Теорема о сходимости метода Ньютона. Способы подбора начальной точки итерационного процесса.

8. Решение нелинейных уравнений методом простой итерации.

9.Теоремы о сходимости метода простой итерации.

10. Решение нелинейных уравнений методом Рыбакова.

11. Доказательство сходимости метода Рыбакова.

12. Решение систем нелинейных уравнений методом Ньютона.

13. Аппроксимация функций: обзор основных методов.

14. Численное дифференцирование. Вычисление производных с помощью конечных разностей.

15. Интерполяция с помощью многочлена Лагранжа. Оценка погрешности интерполяции

16. Интерполяция с помощью многочлена Ньютона. Оценка погрешности интерполяции.

17. Численное интегрирование: метод трапеций. Оценка погрешности

интерполяции.

18. Численное интегрирование: метод Симпсона. Оценка погрешности.

19. Правило Рунге, особенности его применения для задач

численного интегрирования.

20. Автоматический выбор шага интегрирования.

21. Задача Коши, обзор основных способов ее решения.

22. Численное решение обыкновенных дифференциальных уравнений: метод Эйлера.

23. Численное решение обыкновенных дифференциальных уравнений: метод Рунге-Кутта.

24. Метод наименьших квадратов.

25. Метод прогонки.

26. Решение обыкновенных дифференциальных уравнений с помощью метода последовательных приближений.

27. Решение обыкновенных дифференциальных уравнений с помощью разложения в ряд Тейлора.

28. Краевые задачи, обзор основных способов их решения.

29. Решение краевой задачи с помощью конечных разностей.

30. Правило Рунге, особенности его применения для задач

решения обыкновенных дифференциальных уравнений.

31. Теорема о матрице с диагональным преобладанием.

32. Особенности численного вычисления несобственных интегралов. Примеры.

1. Метод Гаусса

[править]

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Метод Гаусса (оптимизация).

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Содержание   [убрать]  1 История 2 Описание метода 2.1 Условие совместности 2.2 Алгоритм 2.2.1 Описание 2.2.2 Простейший случай 2.3 Пример 3 Применение и модификации 4 Достоинства метода 5 См. также 6 Примечания 7 Литература

[править]История

Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах», составленном между I в. до н.э. и II в. н. э.

[править]Описание метода

Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

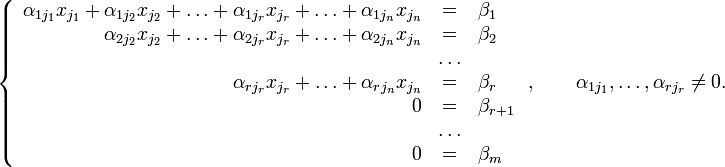
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  ^[3].

Тогда переменные   называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число  , где i > r, то рассматриваемая система несовместна.

Пусть   для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом   ( , где   — номер строки):

, где 

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.

[править]Условие совместности

Упомянутое выше условие   для всех   может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия: Количество главных переменных равно рангу системы и не зависит от её решения. Если ранг совместной системы равен числу переменных данной системы, то она определена.

[править]Алгоритм

[править]Описание

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

• На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

• На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует порядка O(n³) действий.

Этот метод опирается на:

Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.

[править]Простейший случай

В простейшем случае алгоритм выглядит так:

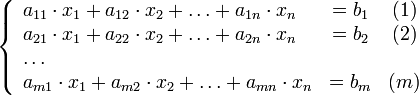
• Прямой ход:

• Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

[править]Пример

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при   во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на   и  , соответственно:

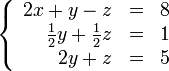
Теперь обнулим коэффициент при   в третьей строке, вычтя из неё вторую строку, умноженную на  :

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные   и  .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

[править]Применение и модификации

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:

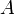• нахождения матрицы, обратной к данной (к матрице справа приписывается единичная такого же размера, что и исходная:  , после чего   приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица:  );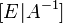

• определения ранга матрицы (согласно следствию из теоремы Кронекера—Капелли ранг матрицы равен числу её главных переменных);

• численного решения СЛАУ в вычислительной технике (ввиду погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).

[править]Достоинства метода

• Менее трудоёмкий по сравнению с другими методами.

• Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.

• Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы^[4].