50. Зависимости для определения коэффициента Шези С для квадратичной области;

Формула1 наз фор Шези.

V-средняя скор. В дан жив. сеч. R-гидр. рад.; J-пьезом. уклон С-коэфициент Шези. Формулы связывают коэффициент гидравлического трения Л и коэффициент Шези С. Как видно, зная Л, легко найти С. Поскольку Л является безразмерным коэффициентом, то коэффициент Шези, имеет размерность. Размерность С равна корню квадратному из размерности ускорения.

Так как Л для квадратичной области сопротивлений зависит только от относительной шероховатости стенок русла и не зависит от числа Рейнольда, а следовательно, и от рода жидкости, движущейся в русле, то в отношении С мы можем сказать то же самое: С зависит от относительной шероховатости стенок русла и не зависит от скорости движения V и вязкости жидкости, т. е. от коэффициента v (разумеется, если формулу Шези мы будем распространять и на область доквадратичного сопротивления, то в пределах этой области величина С окажется зависящей от R.е).

Надо учитывать, что формула Шези (4-95), строго говоря, может исполь­зоваться только для квадратичной области сопротивлений в случае установившегося равномерного движения жидкости в руслах так называемого «правильного» поперечного сечения (см. выше).

Зависимости, вытекающие из формулы Шези. Исходя из формулы |Ш можно получить следующие практически важные расчетные зависимости:

Ф-2

51. Перечень наиболее употребительных формул при гидравлического коэффициента трения;

53.Резкое расширение. Формула Борда. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора.

Рассмотрим внезапное расширение трубы с горизонтальной осью. Потеря напора на внезапное расширение равна

. (103)

Разность давлений найдем, применив уравнение количества движения к отсеку жидкости между сечениями 1-1 и 2-2. За время t через сечения 1-1 и 2-2 протечет масса жидкости , количество движения которой в сечении 1-1, где скорость равно , а в сечении 2-2 – , т. к. , то изменение количества движения протекшей массы составит

. (а)

Это изменение количества движения равно импульсу сил давления. Эти силы следующие: в сечении 1-1, где давление , сила давления направлена в сторону течения и равна (считается, что давление действует и на поперечной стенке). Сила давления в сечении 2-2 направлена против течения и равна . Суммарный импульс этих сил за время t составляет

. (б)

В соответствии с теоремой о количестве движения приравниваем выражения (а) и (б)

Отсюда после деления на и на и перемены знаков получаем

, (104)

так как .

Подставляя правую часть равенства (б) в выражение (а), имеем

, (105)

или окончательно

, (106)

т. е. потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Уравнение (106) называется формулой Борда.

Для выявления значения коэффициента местного сопротивления из уравнения (106) вынесем за скобки

,

или

. (107)

Заменяя скорости через площади живых сечений из уравнения неразрывности , получим

. (108)

54. Местные потери напора на выходе из трубопровода;

70. Истечение жидкости через отверстия в тонкой стенке при постоянном напоре в атмосферу;

Отверстия в гидравлике делятся на малые и большие.

Малые – отверстия, в различных точках которого геометрический напор одинаков.

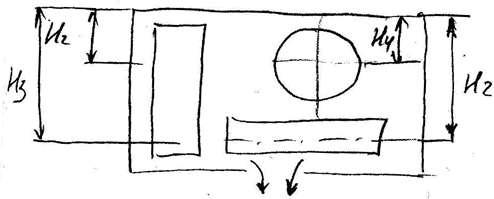
Форма отверстий во многих случаях существенно сказывается на параметрах вытекающего потока и его формы. Изменение формы стекающей струи жидкости относительно отверстия называется инверсией жидкости.

Отверстия могут выполняться в тонкой или толстой стенке. Стенка считается тонкой, если её толщина S<2/3 напора. Толстая стенка, если S>2/3 напора.

Явление сжатия струи через отверстие в тонкой стенке на определенном расстоянии:

- коэффициент сжатия струи

Сжатие называют совершенным, если боковые стенки сосуда не влияют на истечение струи.

Полное – сжатие по всему периметру

Если H=const, то это стечение при постоянном напоре

Свободное стечение жидкости – истечение жидкости в атмосферу.

Скорость и расход жидкости : ,

Скорость для реальной жидкости корректируется с помощью коэффициентов , - коэффициент скорости.

Для расхода: , - коэффициент расхода