Многомерные векторные с.В.

Многомерной с.в. или случайным вектором называется упорядоченная совокупность скалярных

с.в. где 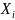- координата случайного вектора.

Пусть - с.в. заданные на вероятностном пространстве (Ω,А,Р) каждому элементарному событию эти с.в. ставят в соответствие n-мерный вектор ( ).

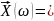Опр: отображение Ω →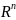 задаваемое с.в. называется случайным вектором или многомерной с.в.

Векторную с.в. заданную на вероятностном пространстве (Ω,А,Р) можно представить как совокупность измеримых функций ( ).

Векторная ф-я 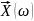ставит в соответствие некоторой точке из Ω некоторую точку из

Векторная с.в. считается заданной если задана область её возможных значений и закон распределения.

Измеримость ф-ий позволяет определить вероятность того что векторная с.в. принадлежит некоторому множеству В:

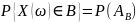
Ф-я распределения многомерной с.в. и её основные свойства.

Ф-ей распределения n-мерного случайного вектора или ф-ей совместного распределения

с.в. называется неслучайная ф-я n действительных переменных определяемая как вероятность совместного выполнения n неравенств:

В частном случае для двухмерного случайного вектора (Х,У) имеем

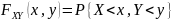
Свойства:

1.

2. - условия

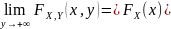согласованности

3. - условие нормировки

4. - неубывающая ф-я своих аргументов

5. - непрерывная слева по каждому из аргументов

6. Вероятности попадания случайной точки на плоскости (Х,У) в прямоугольник со сторонами параллельными осям координат может быть вычислена по формуле:

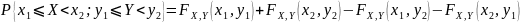
23. Многомерная плотность вероятности.

Многомерная плотность распределения.

Если компоненты вектора - непрерывные с.в. то может быть определена многомерная плотность вероятности этого вектора.

Опр: плотность распределения случайного вектора или плотность совместного распределения называется n-мерная смешанная частная производная ф-ии распределения, взятая один раз по каждому аргументу:

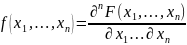
Свойства:

1.

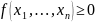
2.

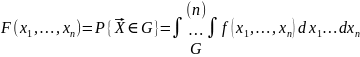
3. - условие нормировки

3. - свойство согласованности

т.о. из многомерной плотности вероятности можно найти одномерную для ∀ компоненты вектора

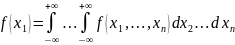
Элементом вероятности для системы с.в. 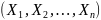в точке 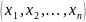называется величина приближённо равная вероятности попадания в элементарную область n-мерного пространства с размерами примыкающую к точке т.е.

Вероятность попадания случайной точки в произвольную область D выражается n-кратным интегралом по D:

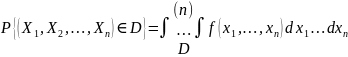
24. Многомерные вероятности.

Если все компоненты вектора - д.с.в.

то можно задать многомерную вероятность этого вектора так:

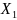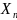P( ,…, )=P( = , … , = ) (1)

Если число возможных значений координат вектора конечно, то вероятности (1) можно представить в виде многомерных таблиц.

Свойства:

1 P( )

2 - условие нормировки

3

25. Независимость случайных величин.

Опр: с.в. называется независимыми, если для набора событий ,где подмножества числовой прямой ,выписывается равенство:

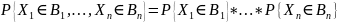
След. теорема также может служить определением независимости с.в.

Тh1: с.в. независимы тогда и только тогда, когда в любой точке соблюдается равенство

Если с.в. непрерывны, то важный критерий непрерывности содержится в теореме 2.

Th2: пусть с.в. имеют плотности , тогда для независимости с.в. необходимо и достаточно ,чтобы плотность вектора 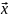равная (3)

Если д.с.в. то условие независимости запишется в виде:

26. Условный закон распределения. Условная плотность.

Опр: пусть 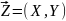–случ. вектор. Условным законом распределения одной из координат этого вектора наз-ся её з-н. распр-я, вычисленный при усл. что другая случайнаяя координата приняла определённое значение или попала в какой-то интервал

– условная вероятность, т.е. это вер-ть события при условии что она может быть названа условной ф-ей распр-я с.в. при условии

Обозначим это условная ф-я распределения, тогда

(1)

Если в качестве первой координаты взять с.в. то по аналогии с (1) получим

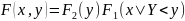(2)

На практике применяют другой вид усл. закона распр-я: закон распр-я одной из с.в.при условии, что другая приняла вполне опр-е зн-е.

Вычислим такой закон для истины двух д.с.в. Он образован усл. вероятностями

или

эти усл. вер-ти найдем по след. формуле:

эту ф-лу применим для нахождения усл. вер-ти того, что с.в. 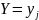при усл. что

(3)

(4)

Совокупность вер-тей (3) для представляет собой условный ряд распр-я с.в.

при усл. что .Аналогично для форм. (4).

Этот ряд обладает св-ми обычного ряда распр-я, а именно: образующих вер-тей равна 1