Основные свойства плотности распределения:

1) плотность распределения неотрицательная ф-ия f(x) ≥ 0, это свойство следует из определения плотности: производная неубывающей функции не может быть отрицательной.

2) - условие нормировки.

Док-во: это свойство следует из формулы (4), если положить в ней x>+∞ и учесть что F(+∞) =1.

Геометрически эти св-ва плотности f(x) интерпретируются так:

1) вся кривая распределения лежит не ниже 0x

2) полная площадь ограниченная кривой распределения и 0x равна 1.

19. Примеры законов распределения непрерывной случайной величины.

Равномерное распределение

Это распределение при котором все значения с.в. в области её существования (н-р интервале [a,b]) равновероятны.

Ф-я распределения для такой с.в. имеет вид:

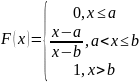
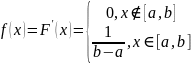
M(x)= ; D(x)=

Нормальное распределение (з-н Гаусса)

Это распределение имеет место когда на формирование с.в. сказывается влияние мн-во разнообразных но одинаковых по своему воздействию факторов.

С.в. X называется нормальной если её плотность вероятности имеет вид:

f(x)=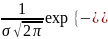

M(x)=a; D(x)=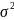

Если a=0 и σ=1 то распределение называется стандартным.

Показательное распределение.

Распределение непрерывной случайной величины X называется показательным (экспоненциальным), если плотность вероятности этой величины описывается функцией:

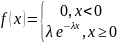
Соответственно функция распределения имеет вид: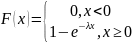

M(x)=1/λ; D(x)=1/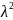

Распределение Релея:

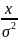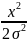f(x)= exp{- }, x≥0, σ>0

F(x)=1- exp{- }, x≥0

M(x)= 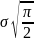; D(x)=2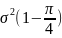

20. Числовые характеристики случайных величин (мат. ожидание и его свойства, дисперсия и её свойства).

Достаточно на практике указать отдельные числовые параметры, характеризующие существенные числовые параметры:

1) Среднее - вокруг которого разбросаны значения с.в.

2) Число характеризующее величину этого разброса

Опр1 числа в сжатой форме выражающие наиболее существенные черты распределения на-ся числовыми характеристиками.

Мат. Ожидание.

Опр2 мат. ожиданием или средним значением с.в. X заданной на вер-ом пр-ве (Ω,A,P) называется число M[X]=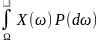 = 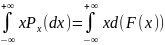(1)

Из определения м.о. следует что M[X] всегда ∃ если M|[X]|<∞

Если F(X) ступенчатая ф-я, т.е. рассматривается д.с.в., то интеграл (1) превращается в сумму M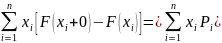[x]= ; P{x= }=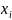

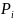
Основные cсвойства мат. Ожиданий

1. Для ∀ константы C: M[CX]=CM[X] и M[C]=C

2. Если а и b = const , то M[a+bX]=a+bM[X]

3. М.о. двух с.в. равно сумме м.о. слагаемых M[X+Y]=M[X]+M[Y],

это сво-во обобщено для n слагаемых: M[X1+…+Xn]=M[X1]+…+M[Xn]

4. М.о. произведения 2х независимых с.в. равно произведению их м.о. M[XY]=M[X]M[Y],

это сво-во обобщено для n множителей: M[ ]=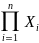

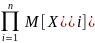
Опр3 модой с.в. наз-ся её наиболее вероятное значение, т.е. для которого вероятность Pi или плотность расп-я f(x) достигает максимума.

Если или f(X) достигает максимума в нескольких точках, то распределение н-ся полимодальным

Опр4 медианой непрерывной с.в. X н-ся такое её значение что P{X<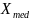 }= P{X> }=1/2 Т.е. одинаково вероятно окажется ли с.в. больше или меньше .

Для симметричных распределений M[X], 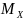- мода и совпадают.