
- •Предмет тв.
- •Построение вероятностной мат. Модели случайного явления.
- •Классификация событий.
- •Действия над событиями.
- •Свойства действий над событиями.
- •Вероятность и её свойства.
- •Аксиомы вероятности (Колмогорова)
- •Геометрическое определение вероятности.
- •Статистическое определение вероятностей.
- •Th1. Умножение вер-ей.
- •Th2. (обобщение Th умножения на n событий).
- •Свойства независимых событий:
- •Формула полной вероятности
- •Формула Байеса.
- •Основные свойства плотности распределения:
- •Показательное распределение.
- •Распределение Релея:
- •Мат. Ожидание.
- •Основные cсвойства мат. Ожиданий
- •Дисперсия с.В.
- •Свойства дисперсии:
- •Моменты с.В.
- •Квантиль распределения.
- •Многомерные векторные с.В.
- •Многомерная плотность распределения.
- •Свойства:
- •Свойства:
- •Теорема умножения плотностей.
- •Основные свойства этой матрицы.
- •Основные свойства этой матрицы
- •1. Непрерывная с.В. Φ (X) – монотонная
- •2. Непрерывная с.В. Φ (X) не монотонная функция
- •Определение и свойства характеристической функции
- •Свойства характеристической функции:
- •Свойства характеристических функций векторных с.В.:
- •Свойства производящей функции:
Геометрическое определение вероятности.
Это определение используется, когда опыт имеет несчётное множество равновозможных исходов.
В этом случае пространство элементарных событий можно представить в виде некоторой области G.
∀ точка этой области соответствует элементарному событию
Попадание наугад брошенной точкой в ∀ место области G равновозможно.
Если
некоторому событию А соответствуют
точки, составляющие некоторую область
С внутри G
то вероятность
 где mesG
- мера области G
(длинна, площадь, объём…)
где mesG
- мера области G
(длинна, площадь, объём…)
Геометрическое определение вероятностей удовлетворяет аксиомам Колмогорова и является частным случаем аксиоматического определения.
7. Статистическое определение вероятности.
Статистическое определение вероятностей.
Наиболее часто встречаются сложные случайные явления с неравновозможными исходами в опыте. Наблюдая за такими явлениями в повторяющихся опытах можно установить, что ∃ объективная характеристика степени возможности появления случайного события, которая проявляется в частоте появления события.
Многократно
(m-раз)
проводится опыт. Событие А появляется
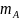 раз. Частота появления события
раз. Частота появления события
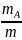
При m>>1 частота сохраняет постоянную величину. На этом основано статистическое определение вероятностей.

Это определение удовлетворяет аксиомам Колмогорова и пригодно во всех случаях.
8. Условная вероятность.
Пусть задано вероятностное пространство (Ω, F, P) и на нём произвольные события A и B.
Если
P(B)>0,
то условная вероятность события А есть
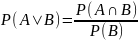
Вероятность события А - это мера объективной возможности данного события при определённых условиях опыта.
Совокупность условий опыта обозначается γ. Вероятность события А: Р(А) = Р(А|γ)
Обычно условия опыта в обозначениях вероятностей не используются. Они оговариваются при проведении опыта. Р(А) называется безусловной вероятностью.
Допустим, что при данных условиях γ произошло событие В. Наступление события В можно считать дополнительным условием.
Вероятность наступления А при совокупности условий (γ,В) и есть условная вероятность.
Р(А|B)=P(A|γ ,B)
Разница между условной и безусловной вероятностями состоит в различии совокупных условий.
Безусловная вероятность есть частный случай условной, если условие В - достоверное.
Определение условной вероятности удовлетворяет аксиомам Колмогорова:
А1.
 ,
т.к.
,
т.к.
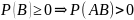
А2.
 ,
т.к.
,
т.к.
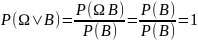
А3.
Если A
и C
– несовместные, т.е. А ⋂С
то
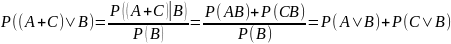
9. Свойства условных вероятностей.
1) P(B|B) = 1
Док-во:
P(B|B)
=
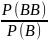 =
=
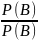 = 1;
= 1;
2)
P( |B)
= 0
|B)
= 0
Док-во: P( |B) = = = 0;
3) Если B с А, то P(A|B) = 1
Док-во:
P(A|B)
=
 =
=
4) P(A|B) + P(A̅|B) = 1
Док-во:
P(A|B)
+ P(A̅|B)
=
 =
=
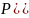 = 1;
= 1;
5) P(AUC | B) = P(A|B) + P(C|B) – P(AC|B)
Док-во: представим в виде несовместных событий
A U C = A + A̅C; C = AC + A̅C; P(A U C | B) = P(A|B) + P(A̅C|B) (*).
P(C|B) = P(AC|B) + P(A̅C|B); P(A̅C|B) = P(C|B) – P(AC|B) подставим в (*)
получим P(AUC|B) = P(A|B) + P(C|B) – P(AC|B);
Th1. Умножение вер-ей.
Пусть задано вер-е пр-во (Ω, A, P) и на нём определены соб-я A и B, P(A)>0 P(B)>0.
Тогда вероятность совместного появления событий A и B равна произведению вероятности одного из этих событий и условной вероятности другого, при условии, что первое произошло:
P(AB) = P(A)P(B|A) = P(B)P(A|B) (2);
Док-во:
по опр-ю цел-й вер-ти P(A|B)
=
,
P(B|A)
=

Замечание: ф-ла (2) применима и в том случае, когда одно из событий невозможное,
например: P(A) = 0 P(A|B) = 0 P(AB) = 0
