
- •Предмет тв.
- •Построение вероятностной мат. Модели случайного явления.
- •Классификация событий.
- •Действия над событиями.
- •Свойства действий над событиями.
- •Вероятность и её свойства.
- •Аксиомы вероятности (Колмогорова)
- •Геометрическое определение вероятности.
- •Статистическое определение вероятностей.
- •Th1. Умножение вер-ей.
- •Th2. (обобщение Th умножения на n событий).
- •Свойства независимых событий:
- •Формула полной вероятности
- •Формула Байеса.
- •Основные свойства плотности распределения:
- •Показательное распределение.
- •Распределение Релея:
- •Мат. Ожидание.
- •Основные cсвойства мат. Ожиданий
- •Дисперсия с.В.
- •Свойства дисперсии:
- •Моменты с.В.
- •Квантиль распределения.
- •Многомерные векторные с.В.
- •Многомерная плотность распределения.
- •Свойства:
- •Свойства:
- •Теорема умножения плотностей.
- •Основные свойства этой матрицы.
- •Основные свойства этой матрицы
- •1. Непрерывная с.В. Φ (X) – монотонная
- •2. Непрерывная с.В. Φ (X) не монотонная функция
- •Определение и свойства характеристической функции
- •Свойства характеристической функции:
- •Свойства характеристических функций векторных с.В.:
- •Свойства производящей функции:
Свойства производящей функции:
По пр. функции распределение восстанавливается однозначно по формуле:
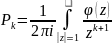 dz
, k=1,2, …
dz
, k=1,2, …
Или по формуле:
=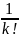
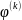 (0)
(0)
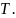 е.
отображение
е.
отображение
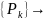 𝜑(z),
|z|≤1
является взаимно-однозначным.
𝜑(z),
|z|≤1
является взаимно-однозначным.
Пр. функция связана с характеристической функцией соотношением (t)=
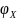 (
(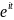 )
)Усл. нормировки 𝜑(1)=1
С помощью производящей функции можно вычислять мат. ож.
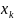 =k,
∀k;
𝜑’(1)=M[X]
=k,
∀k;
𝜑’(1)=M[X]
Док-во:
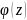 =
;
𝜑’(z)
=
;
𝜑’(z) =
=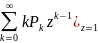 =
=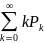 =M[X]
=M[X]
M[ ]= 𝜑’’(1)+ 𝜑’(1)
Док-во:
пусть
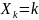 для
∀k,
для
∀k,
𝜑’’(z)=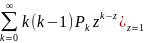 =
=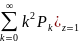 -
-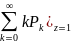 =
M[
]-M[X]
=
M[
]-M[X]
т.к. по св-ву (4) M[X]= 𝜑’(1), то M[ ]= 𝜑’’(1)+ 𝜑’(1)
У= где – независимая д.с.в. принимающая значения из множества N={????}
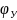 (z)=
(z)=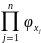 (z)
(z)
Док-во:
(z)=M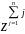 =
=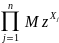 =
(z)
=
(z)
38. Виды сходимости последовательностей случайных величин.
Пусть
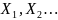 - послед-ть с.в. заданная на вероятностном
пространстве
- послед-ть с.в. заданная на вероятностном
пространстве
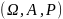
Пусть на этом пространстве задана с.в. X
Опр1:
послед-ть с.в.
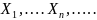 наз-ся сход-ся по вероятности к с.в. X
если для
наз-ся сход-ся по вероятности к с.в. X
если для
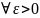 вер-ть
вер-ть
 (1)
(1)

Опр2: послед-ть с.в. сходится почти наверное (почти всюду ,с вер-тью 1) и с.в. X если
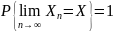 (2) т.е
(2) т.е
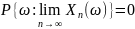 это означает, что мн-во исходов
это означает, что мн-во исходов
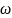 для которых
для которых
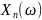 не сходится к
не сходится к
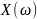 имеет нулевую вер-ть
имеет нулевую вер-ть
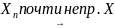
Опр3:
посл-ть с.в.
наз-ся сходящейся в среднем порядка
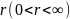 к с.в. X
к с.в. X
если
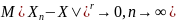 (3)
(3)
если
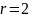 то сх-ть (3) наз-ся сходимостью в среднем
квадратическом.
то сх-ть (3) наз-ся сходимостью в среднем
квадратическом.
Сходимость
в среднем порядка
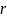 обозначается
обозначается
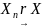
Опр4:
посл-ть с.в.
наз-ся сходящейся по распределению к
с.в. X
если во всех точках x
где F(x)
непрерывна вып-ся усл.:
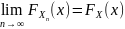 (4)
(4)
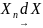
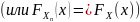
39. Центральная предельная теорема.
Th: пусть – послед –ть независимых, одинаково распределенных с.в. с мат. ож-ием
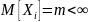 и дисперсией
и дисперсией

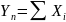 тогда при
тогда при
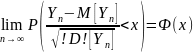 (1)
(1)
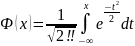 ф-я стандартного
норм. распр-я.
ф-я стандартного
норм. распр-я.
Док-во:
пусть
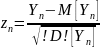 ,
,
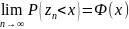 утв-е теоремы означает, что
утв-е теоремы означает, что
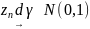 (нормальный закон
распр-я)
(нормальный закон
распр-я)

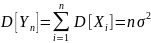 подставим в
подставим в
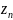
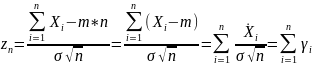
Пусть
 – характерист. ф-я центрированной с.в.
тогда
– характерист. ф-я центрированной с.в.
тогда
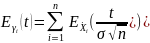
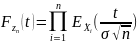 (*) разложим
характеристич. ф-ю в ряд Макларена:
(*) разложим
характеристич. ф-ю в ряд Макларена:
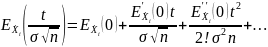
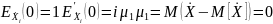
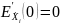
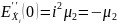
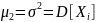
Подставляем
в разложение
 подставим в (*)
подставим в (*)
 – характ. ф-я с.в.
– характ. ф-я с.в.
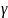 распределенной по нормальному закону
с
распределенной по нормальному закону
с
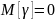 и
и
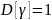
по теореме единственности однозначное соответствие между
xарактеристич. ф-ей и ф-ей распр-я.
Т.о.

40. Интегральная теорема Муавра-Лапласа.
Является следствием из центральной предельной теоремы
Теорема:
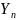 - суммарное число успехов в n
испытаниях по схеме Бернулли с вер-ю
успеха р и вер-ю неудачи q
= 1-p.
Тогда с ростом n
пос-ть ф-ии распределения случайной
величины
- суммарное число успехов в n
испытаниях по схеме Бернулли с вер-ю
успеха р и вер-ю неудачи q
= 1-p.
Тогда с ростом n
пос-ть ф-ии распределения случайной
величины
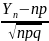 сходится по распределению функции
стандартного нормального распределение,
т.е.
сходится по распределению функции
стандартного нормального распределение,
т.е.
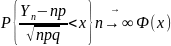
Док-во:
Пусть - число успехов в испытании Бернулли.
Тогда
M[
]
= p,
D[
]
= pq.
Представим
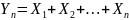 и,
используя утверждение центральной
предельной теоремы (
,
где
ф-я стандартного норм.распр-я ),
приходим к утверждению теоремы.
и,
используя утверждение центральной
предельной теоремы (
,
где
ф-я стандартного норм.распр-я ),
приходим к утверждению теоремы.
41. Закон больших чисел: не-во Чебышева, теоремы Чебышева, Хинчина, Маркова.
Нер-во
Чебыышева: Лемма: Пусть (Ω,
A, P) – вер-е пр-во. Пусть есть с.в. Х с м.о.
и
дисперсия
тогда ∀ℇ>0
справедливо P(|x-
|≥
ℇ)≤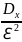 (1) нер-во Чеб-шева, оно утверждает, что
∀ℇ>0
вер-ть того, что с.в. отклонится от своего
мат. ож. Не меньше, чем на
ℇ,
ограничена
сверху величиной
.
(1) нер-во Чеб-шева, оно утверждает, что
∀ℇ>0
вер-ть того, что с.в. отклонится от своего
мат. ож. Не меньше, чем на
ℇ,
ограничена
сверху величиной
.
З-н больших чисел: Под этим назв-ием в т.в. ∃ группа Т., утверждающих, что среднее арифметич. с.в. сходится по вер-ти и неслучайной велич. при неограниченномувелич-ии числа слога-ых.
Т.
Чебышева: (збч) Если
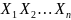 посл-тьнезвав-ыходинакого
распределённых с.в. имеющих конечные
дисперсии, ограниченной одной и той же
постоянной D[
посл-тьнезвав-ыходинакого
распределённых с.в. имеющих конечные
дисперсии, ограниченной одной и той же
постоянной D[ ]≤C…D[
]≤C…D[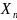 ]≤C,
то ∀ℇ>0
]≤C,
то ∀ℇ>0
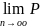 {|
{|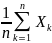 -
- |<ℇ}=1
|<ℇ}=1
Д-во:
в условиях теоремы D[
]=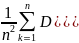 ]=>D[
]≤
]=>D[
]≤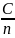 согласно нер-ву Чебышева (1) имеем P{|
-
|<ℇ}≥1-
согласно нер-ву Чебышева (1) имеем P{|
-
|<ℇ}≥1-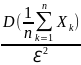 ≥1-
≥1-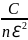 переходя к пределу получаем:
переходя к пределу получаем:
{| - |<ℇ}≥1, а т.к. вер-ть не может быть >1, то =1
Т.
Хинчина: Если посл-ть попарно независимых
с.в.
такова, что M[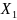 ]=…=
M[
]=m
]=…=
M[
]=m
D[
]≤…
≤D[
]≤cто∀ℇ>0
{|
-
m|<ℇ}=1
– это есть усл-иесх-ти по вер-ти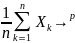 m
m
Этот частный случай Т.Чеб-ва даёт основания правилу среднего арифметического.
Т.
Маркова (з.н. бол-их чисел в общей
формул-ке): Если посл-ть произвольных
с.в.
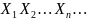 такова, что при n
такова, что при n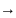 oo
oo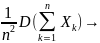 0,
то ∀ℇ>0
{|
-
|<ℇ}=1
0,
то ∀ℇ>0
{|
-
|<ℇ}=1
Если
с.в.
попарно нез-мы, то усл-е Маркова принимает
вид
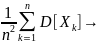 0при
n
oo
0при
n
oo
Из Т.М. видно, что Т.Ч. является её частным случаем.
42. Следствия закона больших чисел: теоремы Бернулли и Пуассона
Т.
Бернулли:
Если событие А происходит в каждом опыте
с вер-ю Р(А)=р, то частота появления этого
события
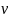 сход-ся
по вер-ти и p
при n
oo
т.е.
сход-ся
по вер-ти и p
при n
oo
т.е.
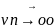 p
p
Д-во:
Рассмотрим независ. с.в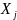 Число
появлений события А в j-ом
опыте
Число
появлений события А в j-ом
опыте
Ряд-распр-я
для д.с.в имеет вид: M[
]=p;
D[
]=pq,
где q=1-p
M[
]=p;
D[
]=pq,
где q=1-p
Усл-ие
Т. Хинчина выполняется =>
=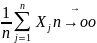 pт.е.
p
pт.е.
p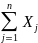 – число появсл-ий события А в nопытах,
деление на nдаёт
частоту
– число появсл-ий события А в nопытах,
деление на nдаёт
частоту
Т. Б-лли утверждает устойчивость частоты при постоянных усл-ях опытов. При переменных условиях опытов так же ∃ устойчивость частоты.
Т.Пуассона: Если производится n- нез. опытов и вер-тьпоявл-я соб-я А в i-ом опыте равна
то
при n
oo
частота
соб-я
А сход-ся по вер-ти и среднему арифметич-ому
т.е.
p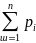
Д-во: с пом-ю Т. Чебышева: Пусть исследования пров-ся многократно, но изм-сяусл-я их проведения. Вер-ть зависит от условий, но сх-ся к средней вер-ти.
