
- •Предмет тв.
- •Построение вероятностной мат. Модели случайного явления.
- •Классификация событий.
- •Действия над событиями.
- •Свойства действий над событиями.
- •Вероятность и её свойства.
- •Аксиомы вероятности (Колмогорова)
- •Геометрическое определение вероятности.
- •Статистическое определение вероятностей.
- •Th1. Умножение вер-ей.
- •Th2. (обобщение Th умножения на n событий).
- •Свойства независимых событий:
- •Формула полной вероятности
- •Формула Байеса.
- •Основные свойства плотности распределения:
- •Показательное распределение.
- •Распределение Релея:
- •Мат. Ожидание.
- •Основные cсвойства мат. Ожиданий
- •Дисперсия с.В.
- •Свойства дисперсии:
- •Моменты с.В.
- •Квантиль распределения.
- •Многомерные векторные с.В.
- •Многомерная плотность распределения.
- •Свойства:
- •Свойства:
- •Теорема умножения плотностей.
- •Основные свойства этой матрицы.
- •Основные свойства этой матрицы
- •1. Непрерывная с.В. Φ (X) – монотонная
- •2. Непрерывная с.В. Φ (X) не монотонная функция
- •Определение и свойства характеристической функции
- •Свойства характеристической функции:
- •Свойства характеристических функций векторных с.В.:
- •Свойства производящей функции:
1. Непрерывная с.В. Φ (X) – монотонная
Имеется непрерывная с.в. X с плотностью вероятностей f(X), с.в. Y= φ (x) (1). Требуется найти закон распределения с.в. Y. Пусть φ (x) – строго монотонна, непрерывна и дифференцируема в интервале (a,b) всех возможных значений с.в. X. Функция распределения с.в. Y определяется по формуле G(Y)=P{Y<y} (2) Пусть функция φ (x) монотонно возрастает на всем участке возможных значений с.в. X
Из графика
видно что событие {Y<y} эквив-но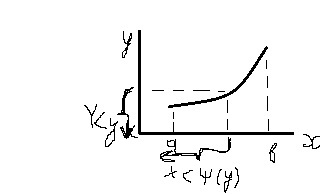 событию {X< ψ(y)}, где ψ(y)=x – функция,
обратная к функции φ (x)=y. Из строгой
монотонности φ (x) следует однозначность
функции ψ(y). G(y)=P{Y<y}=P{X< ψ(y)}=
событию {X< ψ(y)}, где ψ(y)=x – функция,
обратная к функции φ (x)=y. Из строгой
монотонности φ (x) следует однозначность
функции ψ(y). G(y)=P{Y<y}=P{X< ψ(y)}= (3) Дифференцируя (3) по y, входящей в
верхний предел интеграла получим
плотность распределения с.в. Y. g(y)=
(3) Дифференцируя (3) по y, входящей в
верхний предел интеграла получим
плотность распределения с.в. Y. g(y)= (4) Если φ (x) на (a,b) монотонно убывает,
то событие {Y<y} эквивалентно событию
{X> ψ(y)}.
(4) Если φ (x) на (a,b) монотонно убывает,
то событие {Y<y} эквивалентно событию
{X> ψ(y)}.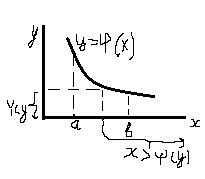 G(y)=
G(y)= (5).
Дифференцируем (5) по y и получим g(y)=
(5).
Дифференцируем (5) по y и получим g(y)=
 (6) плотность распределения. Так как
плотность не может быть <0 то формулы
(4) и (6) можно объединить: g(y)=f(ψ(y))*
(6) плотность распределения. Так как
плотность не может быть <0 то формулы
(4) и (6) можно объединить: g(y)=f(ψ(y))*
*|ψ’(y)| (7)
2. Непрерывная с.В. Φ (X) не монотонная функция
Рассмотрим случай
когда функция φ (x) на (a,b) не монотонна.
В этом случае обратная функция x= ψ(y)
неоднозначна.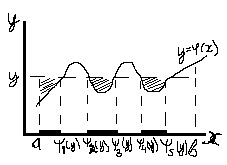 Число
значений обратной функции ψ(y) зависит
от того, какой y мы выбрали.
Обозначим эти значения ψ1(y),
ψ2(y),…,ψi(y)…
Событие {Y<y}
равносильно попаданию с.в. X
в один из не перекрывающихся отрезков,
отмеченных жирной линией, где
соответствующая часть кривой y=φ(x) лежит
ниже прямой y. В нашем случае это будут
отрезки (a;ψ1(y)), (ψ2(y); ψ3(y)),
(ψ4(y); ψ5(y)). Последний отрезок
может кончаться в точке b, а может в одной
из точек ψi(y). Попадание с.в. X в эти
отрезки – события не совместные. По
правилу сложения вероятностей имеем:
G(y)=P{Y<y}=P{X
∈(a,
ψ1(y)}+ P{X
∈(ψ2(y);
ψ3(y))}+ P{X
∈(ψ4(y);
ψ5(y))}+… ; G(y)=
Число
значений обратной функции ψ(y) зависит
от того, какой y мы выбрали.
Обозначим эти значения ψ1(y),
ψ2(y),…,ψi(y)…
Событие {Y<y}
равносильно попаданию с.в. X
в один из не перекрывающихся отрезков,
отмеченных жирной линией, где
соответствующая часть кривой y=φ(x) лежит
ниже прямой y. В нашем случае это будут
отрезки (a;ψ1(y)), (ψ2(y); ψ3(y)),
(ψ4(y); ψ5(y)). Последний отрезок
может кончаться в точке b, а может в одной
из точек ψi(y). Попадание с.в. X в эти
отрезки – события не совместные. По
правилу сложения вероятностей имеем:
G(y)=P{Y<y}=P{X
∈(a,
ψ1(y)}+ P{X
∈(ψ2(y);
ψ3(y))}+ P{X
∈(ψ4(y);
ψ5(y))}+… ; G(y)= …
(1) Учитывая правила дифференцирования
интеграла по переменной, входящей в
него пределы получим : g(y)=f(ψ1(y))
ψ1’(y)-f(a)
…
(1) Учитывая правила дифференцирования
интеграла по переменной, входящей в
него пределы получим : g(y)=f(ψ1(y))
ψ1’(y)-f(a) +
f(ψ3(y)) ψ3’(y)- f(ψ2(y))
ψ2’(y) (2) В тех точках, где φ (x)
пересекла прямую y убывает производная
ψ’(y) отрицательна, где φ (x) возрастает
ψ’(y) положительна. Производные от
постоянных a и b равны 0 поэтому безразлично
фигурируют ли точки a и B в виде конца
или начала. Все члены в формуле (2)
положительны и она принимает простой
вид g(y)=
+
f(ψ3(y)) ψ3’(y)- f(ψ2(y))
ψ2’(y) (2) В тех точках, где φ (x)
пересекла прямую y убывает производная
ψ’(y) отрицательна, где φ (x) возрастает
ψ’(y) положительна. Производные от
постоянных a и b равны 0 поэтому безразлично
фигурируют ли точки a и B в виде конца
или начала. Все члены в формуле (2)
положительны и она принимает простой
вид g(y)= f(ψi(y))|ψi’(y)|
(3) где k-число значений обратной
функции соответствующее данному у
(ψ1(y)… ψk(y))
f(ψi(y))|ψi’(y)|
(3) где k-число значений обратной
функции соответствующее данному у
(ψ1(y)… ψk(y))
x1 |
x2 |
… |
xn |
p1 |
p2 |
… |
pn |
Рассмотрим когда X – д.с.в. с рядом распределения
φ(x1) |
φ(x2) |
… |
φ(xn) |
p1 |
p2 |
… |
pn |
Чтобы сделать из нее ряд распределения нужно:
1) расположить значения, стоящие в верхней строке в порядке возрастания
2) объединить те из них, которые окажутся равными
3) сложить соотв. вероятности
-2 |
-1 |
0 |
1 |
2 |
0.3 |
0.1 |
0.1 |
0.3 |
0.2 |
Пример: дан ряд X, построить ряд распределения Y=X2
4 |
1 |
0 |
1 |
4 |
0.3 |
0.1 |
0.1 |
0.3 |
0.2 |
Y:
|
1 |
4 |
0.1 |
0.4 |
0.5 |

Ряд распределения с.в.Y
вид
34. Характеристические функции. Определение и свойства характеристических функций.
Наряду с вещественными с.в. можем рассматривать и комплексные с.в.
Под комплексной с.в. X будем понимать функцию X=X1+iX2, где X1 и X2 – действит. с.в. (X1,X2) – случайный вектор; M[X]=M[X1]+iM[X2] Рассмотрим комплексные с.в.
x=x1+ix2 y=y1+iy2 Комплексные с.в. X и Y независимы если векторы (x1,x2) и (y1,y2) независимы, т.е. компоненты векторов независимы. M[XY]=M[X]M[Y] если X и Y независимые с.в.

 0
0