1. Предмет ТВ. Построение вероятностной модели случайного явления.

Предмет тв.

ТВ – мат. наука, изучающая закономерности в массовых случайных явлениях.

Случайное явление – явление, которое при неоднократном воспроизведении одного и того же опыта (испытания) протекает каждый раз несколько по-иному.

Закономерности случайных явлений могут проявляться только при их многократном наблюдении.

Изучению поддаются только такие случайные явления, которые можно наблюдать практически не ограниченное число раз. Такие случайные явления называются массовыми.

Результаты отдельных наблюдений случайных явлений непредсказуемы, но при многократном наблюдении выявляются определённые закономерности. Эти закономерности и являются предметом изучения ТВ.

Построение вероятностной мат. Модели случайного явления.

Общим для всех случайных явлений является их непредсказуемость в отдельных наблюдениях.

Для их описания строится математическая вероятностная модель.

Для построения модели введём определения:

Опыт – наблюдение какого-либо явления при выполнении определённых фиксированных условий.

Событие – факт, регистрируемый в результате опыта.

Случайное событие – событие, которое при проведении опыта может произойти, а может не произойти.

События обозначаются заглавными буквами: А, В, С…

Пусть имеется урна с n одинаковыми шарами. Испытание состоит в том, что мы случайно выбираем один шар.

Ω = {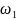 , , … , 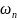} – множество шаров. Если из урны при испытании мы вынимаем шар 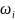∈ А, где А – некоторое подмножество А⊂ Ω, то будем говорить что произошло событие А. Если ∉ А то говорят что событие А не произошло. Событие А отождествляют с подмножеством А множества Ω.

В общем случае любой вероятностной модели будем рассматривать некоторое основное множество Ω={ }. Элементы – элементарные события.

Ω – пространство элементарных событий.

Некоторые его подмножества А⊂Ω – события.

Операции над событиями – операции над подмножествами.

Множество Ω может быть дискретным, непрерывным или иметь сложную структуру.

К дискретным относятся конечные или счётные множества элементарных событий.

К непрерывным – множества типа континуума (пример континуума – конечный или бесконечный интервал на числовой прямой)

Случайное событие А это подмножество А в пространстве элементарных событий Ω.

Подмножество А может содержать один/ни одного/счётное/не счётное число исходов/всё пространство Ω.

2. Случайные события. Действия над событиями, свойства действий.

Классификация событий.

1. Событие А называется невозможным если оно не может произойти в данном опыте. (∅)

2. Событие А называется достоверным если оно обязательно происходит в результате опыта. (Ω)

3. События называются несовместными если в данном опыте ни какие два из них не могут произойти вместе.

4. Событие В называется подсобытием А или частью события А если при появлении события В обязательно происходит событие А. (В ⊂ А)

5. События А и В называется эквивалентными если они могут появиться и не появиться только вместе. (A = B)

6. Событие В = наз-ся противоположным (дополнением) событию А и заключается в не появлении события А.

7. События образуют полную группу событий если в результате опыта обязательно происходит хотя бы одно из них.