7.Электрические цепи постоянного тока со смешанным соединением элементов.

Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю, так как i = const. Если рассматривать конденсатор как идеальную емкость, то в цепи постоянного тока эта ветвь равносильна разомкнутой. Постоянный ток через емкость не проходит. Таким образом, в цепи постоянного тока остаются только источники ЭДС или тока - активные элементы и приемники резисторы - пассивные элементы. Простыми цепями постоянного тока называются цепи с одним источником при последовательном, параллельном и смешанном соединении приемников.

Смешанное соединение это произвольная комбинация последовательных и параллельных соединений. Для каждого смешанного соединения можно найти эквивалентное сопротивление путём последовательных эквивалентных соединений.

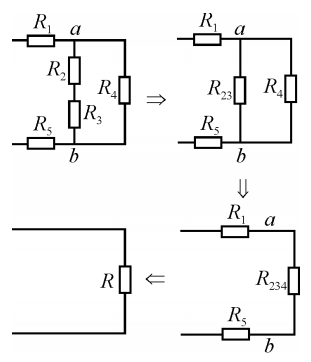
Рассмотрим эту задачу на примере схемы приведенной ниже. Здесь изображены четыре ветви. В первую входит резистор R1; во вторую резисторы R2 и R3; в третью резистор R4 и в четвёртую – R5. Вторая и третья ветви соединены между собой параллельно, т.к. обе соединены с узлами a и b. Однако из этого не следует, что параллельно соединены между собой элементы этих ветвей. Это было бы справедливо только в том случае, если бы обе ветви состояли из одного элемента. На первом этапе эквивалентное преобразование возможно только для последовательного соединения R2 и R3 во второй ветви, т.к. в цепи нет других соединений, которые можно определить как параллельные или последовательные. Теперь каждая из параллельных ветвей состоит из одного элемента, и они образуют между собой параллельное соединение, для которого с помощью выражения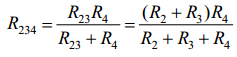 можно найти эквивалентное. В результате мы получили последовательное соединение с эквивалентным сопротивлением.

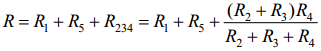
8.Методы расчета электрических цепей

Расчет резистивных цепей методом составления уравнений Кирхгофа. С помощью законов Кирхгофа можно рассчитать токи в сколь угодно сложных цепях. Для этого необходимо проделать следующее: определить количество ветвей в заданной цепи; задаться предполагаемыми токами во всех ветвях и направлениями обходов в контурах (например, по часовой стрелке); по первому закону составитьn-1 уравнений, где n – количество узлов цепи; определить количество элементарных контуров в цепи; составить по второму закону Кирхгофа m уравнений, где m – число элементарных контуров.

 

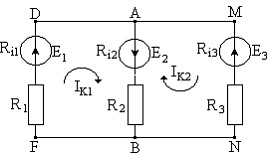
Рис. 1.17. Двухконтурная цепь.

Например, в цепи рис. 1.17 по второму закону Кирхгофа можно составить два независимых уравнения, поскольку элементарных контуров два– FDABF и BAMNB.

Для контура FDABF:                   (1.32)

Для контура BAMNB:                   (1.33)

В полученную систему уравнений подставить числовые значения  и любым методом рассчитать неизвестные в ветвях токи.

Нанести на схему действительные токи с указанием их величин.

Произвести проверку правильности нахождения токов. Для этого следует проверить выполнение первого закона Кирхгофа в узлах, второго закона - в контурах и балансы мощности– во всей цепи. Если все проверки сходятся, то задача решена правильно.

Расчет электрической цепи методом суперпозиции. При применении метода наложения для расчета сложных электрических цепей с несколькими источниками вначале предполагают, что в электрической цепи действует только одна ЭДС, и определяют токи, созданные ею. Эти токи называются частичными. При расчете частичных токов должны учитываться внутренние сопротивления источников, исключенных в этом случае из схемы.

После этого оставляют в электрической цепи какую-либо другую ЭДС и исключают все остальные. При этом опять определяют частичные токи. Таким способом находят поочередно частичные токи, созданные каждой ЭДС отдельно. Затем производят наложение частичных токов, при котором определяют величину и направление действительных токов на основании того, что действительный ток в любом участке электрической цепи равен алгебраической сумме частичных токов, гдеI′ и I″ частичные токи т.е.

                                                          (1.34)

Метод суперпозиции основан на принципе независимости действия электродвижущих сил различных источников. Он применим только к линейным цепям, т.е. таким, сопротивление которых не зависит от величины протекающего тока или приложенного напряжения. Процессы в этих цепях описываются уравнениями первой степени. Если в цепи имеется хотя бы один нелинейный элемент или в выражении, описывающем процессы в цепи, имеется хотя бы одна переменная величина со степенью выше первой, то метод суперпозиции принципиально использован быть не может.

Пусть имеется цепь. (рис. 1.18):

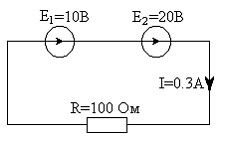
Рис. 1.18. Одноконтурная цепь.

Очевидно, что общий ток в цепи I определяется из выражения

.

Частичные токи, создаваемые источниками Е1 и Е2 определяются выражениями:  и  . Учитывая значения E1, E2 и R, приведенные на схеме будем иметь:

             .

В соответствии с методом суперпозиции имеем:

Расчет электрической цепи методом контурных токов. Метод контурных токов дает возможность определять токи в цепи с помощью стольких уравнений, сколько элементарных контуров имеет цепь.

Контурные токи являются условными алгебраическими величинами, одинаковыми по величине для всех участков данного контура. Направления их выбирают произвольно и показывают в электрических схемах дугообразными стрелками индексами.

Расчет сложной электрической цепи методом контурных токов выполняется в следующем порядке:

1. Произвольно выбирают направление контурных токов, обозначают их и для удобства считают такое же направление обхода по контурам.

2. Составляют уравнения по второму закону Кирхгофа с контурными токами. При этом если на участке цепи действует несколько контурных токов, то падение напряжения на этом участке равно алгебраической сумме падений напряжений, созданных каждым контурным током.

Для определения величины и направления реальных токов применяют правила: 

1. если на участке цепи действует только один контурный ток, то действительный ток равен контурному и имеет такое же направление;

2. если на участке цепи действуют два контурных тока противоположных направлений, то действительный ток равен их разности и направлен в сторону большего тока;

3. если в ветви действуют контурные токи одинакового направления, то действительный ток равен сумме и совпадает по направлению с ними.

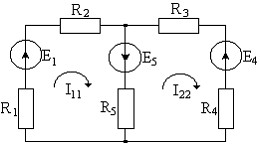
Рис. 1.19. Схема, поясняющая метод контурных токов.

Рассмотрим цепь, изображенную на рис. 1.19. Направление токов в первом и втором контурах I11 I22 обозначим стрелками и запишем уравнение Кирхгофа.

Для первого контура:

     или

.                  (1.35)

Для второго контура:

        или

.                  (1.36)

Введем обозначения:

;         ;

;         ;

.

Тогда уравнения (1.35) и (1.36) примут вид:

;

.                                          (1.37)

где R11 - полное или собственное сопротивление первого контура; R12 – сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; E11 – контурная ЭДС первого контура, равна алгебраической сумме ЭДС этого контура (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура);R22 – полное или собственное сопротивление второго контура; R21 – сопротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; E22 – контурная ЭДС второго контура.

Если в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:

;

;                                  (1.38)

.

Или в матричной форме:

;

где

 

Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например, все по часовой стрелке.

Если в результате решения системы уравнений какой-либо контурный ток окажется отрицательным, то это означает в действительности направление контурного тока обратно принятому за положительное.

Если резистивная цепь содержит k независимых контуров, система уравнений имеет вид:

 

;

 

;

-  -  -  -  -  -  -  -  -  -  -  -  -  -  -  -  -;

.

В уравнении (1.40) слагаемые R1nIkn берутся со знаком «+», если токи Ik1 и Ikn обтекают R1n в одном направлении и со знаком «-» в противном случае. Контурная ЭДС Ek равна алгебраической сумме всех ЭДС, входящих в данный контур. ЭДС, направленные навстречу контурному току, берутся со знаком «+», и со знаком «-», если направления ЭДС и контурного тока совпадают.

Решая систему уравнений (1.40) найдем выражение для контурных токов:

                              (1.41)

где ∆R - определитель системы (1.40), который равен:

 

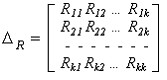
Определитель ∆k находится путем замены k-го столбца в (1.42) правой частью системы (1.40). Например, чтобы получить ∆1 необходимо в (1.42) заменить R11, R21 и Rk1 на Ek1, Ek2 и Ekk соответственно.

Расчет электрической цепи методом эквивалентного генератора. Метод эквивалентного генератора используется для определения тока, напряжения или мощности в одной ветви сложной эквивалентной цепи. При этом всю остальную часть сложной цепи, к которой подключена данная ветвь, представляют в виде двухполюсника.

Различают два метода эквивалентного генератора: метод эквивалентного генератора напряжения и метод эквивалентного генератора тока.

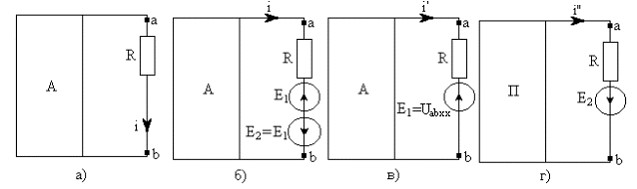
Рис. 1.20 Схемы, поясняющие метод эквивалентного генератора.

Этот метод базируется на теореме Тевенина, согласно которой  по отношению к выделенной ветви при расчете двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника. Докажем теорему:

Пусть задана некоторая схема и требуется найти ток в одной ее ветви. Мысленно заключим всю схему, содержащую ЭДС и сопротивления, в прямоугольник, выделив из нее одну ветвьab, в которой требуется найти ток I (рис. 1.20,а).

Ток I не изменится, если в ветвь ab включить две равные и противоположно направленные ЭДС E1и Е2 (рис. 1.20,б).

На основании принципа наложения ток можно представить в виде суммы двух токов  .

Под током I' будем понимать ток, вызванный ЭДС Е1 и всеми источниками ЭДС и тока активного двухполюсника, заключенными в прямоугольник, а ток I′′ вызывается только одной ЭДС Е2. В соответствии с этим для нахождения токов I′ и I′′ используем схемы рис. 1.20,б,г. В прямоугольнике П схемы рис. 1.20 отсутствуют все ЭДС, но оставлены внутренние сопротивления источников.

ЭДС Е1 направлена встречно напряжению Uab. По закону Ома для участка цепи, содержащего ЭДС  .

Выберем Е1 так, чтобы ток I′ был равен нулю. Отсутствие тока в ветви ab эквивалентно ее размыканию (холостому ходу). Напряжение на зажимах ab при холостом ходе (х.х.) ветви обозначим Uabxx.

Следовательно, если выбрать  , то  . Так как,  , а  , то  . Но ток I″ определяется в соответствии со схемой рис. 1.20 как  . Rвх - входное сопротивление двухполюсника по отношению к зажимам ab.

Метод расчета тока в выделенной ветви, основанный на замене активного двухполюсника эквивалентным генератором, принято называть методом эквивалентного генератора.

1.        при расчете тока этим методом необходимо:

2.        Найти напряжение на зажимах разомкнутой ветви;

3.        Определить входное сопротивление Rвх всей схемы по отношению к зажимам ab при закороченных источниках ЭДС;

4.        Определить ток по формуле:

.                                                          (1.43)

Где R — сопротивление ветви ,в которой определяется ток.