21. Устойчивость нулевого решения нелинейной системы оду по первому приближению.

Решение задачи Коши (21), (22) называется положением равновесия, если .

В этом пункте рассмотрим устойчивость нулевого решения однородной линейной системы

и предположим, что является её положением равновесия. Из этого предположения сразу следует, что . Поэтому если каждая координата вектора непрерывно дифференцируема в окрестности , то её можно разложить по формуле Тейлора до первого порядка с остаточным членом в форме Пеано: . Тогда

Где матрица с постоянными элементами . В этих обозначениях система перепишется в виде ,

Теорема Пусть в некоторой окрестности точки представима в виде: и , где , при .Тогда справедливы следующие утверждения

1. Если для всех собственных чисел матрицы A 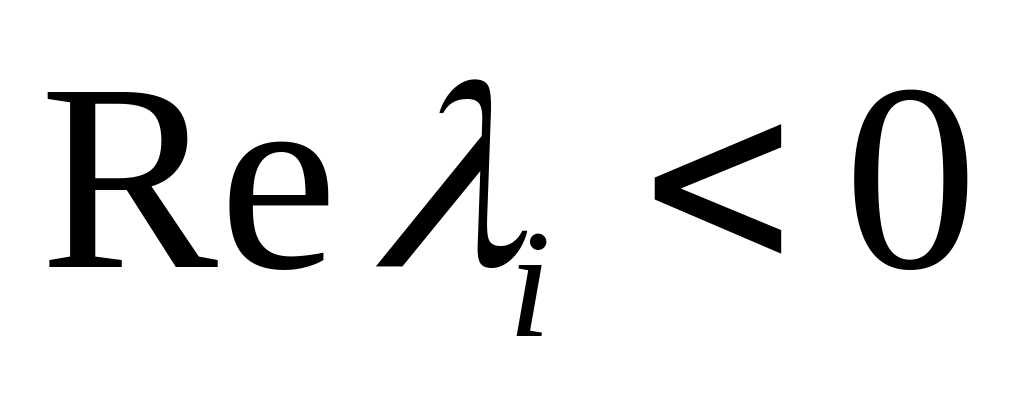, то нулевое решение системы , асимптотически устойчиво.

2. Если собственное число матрицы A, для которого , то нулевое решение системы , неустойчиво.

3. Наконец, если , то устойчивость или неустойчивость нулевого решения системы , зависит не только от матрицы A, но и от функции , и информации о собственных числах для определенного ответа не достаточно.

Пример: Исследовать на устойчивость нулевое решение системы

Разложим правую часть каждого уравнения системы по формуле Тейлора: =

=

Отсюда Составим хар уравнение: , его корни . Поскольку дискриминант подкоренного выражения отрицателен при всех : , .

Таким образом:

1. и нулевое решение системы асимптотически устойчиво;

2. и нулевое решение системы неустойчиво;

3. и устойчивость нулевого решения по первому приближению исследовать невозможно.

22. Устойчивость и асимптотическая устойчивость решения системы оду. Положения равновесия. Сведение к исследованию нулевого решения.

Рассмотрим систему ОДУ: (21). Пусть - решение этой системы, и при оно удовлетворяет начальным условиям (22). Наряду с задачей Коши рассмотрим возмущённую задачу Коши: (23). Решение задачи Коши (21), (22) называется устойчивым по Ляпунову, если при малых возмущениях начальных условий решение задачи Коши меняется мало: . Для решения возмущённой задачи Коши (23) справедлива оценка . Решение задачи Коши (21), (22) называется асимптотически устойчивым, если при малых возмущениях начальных условий решение задачи Коши меняется мало и при больших t неограниченно приближается к решению невозмущённой задачи:

3. Решение задачи Коши(21), (22) является устойчивым по Ляпунову

4. Решение возмущённой задачи Коши(23) приближается к : .

Решение задачи Коши (21), (22) называется положением равновесия, если0 . Из определения видно, что если решение в какой-то момент времени

совпало с положением равновесия, то уйти из него оно уже не сможет: . Поэтому определение можно переписать в виде Решение задачи Коши (21), (22) называется положением равновесия, если .

Лемма: Устойчивость/асимптотическая устойчивость положения равновесия системы (21) эквивалентна устойчивости/асимптотической устойчивости нулевого решения системы

Док: Проведём в системе (21) замену . Тогда , и система (21) переписывается в виде Вывод: при изучении вопросов устойчивости положений равновесия систем ОДУ достаточно ограничиться исследованием устойчивости нулевого решения.

23. Устойчивость и асимптотическая устойчивость решения линейного ОДУ. Сведение к исследованию нулевого решения.

Рассмотрим решение уравнения: (1), удовлетворяющее начальному условию (2). Наряду с задачей Коши (1), (2) рассмотрим возмущённую задачу Коши (3)

задачу для того же уравнения, но с «возмущённым» начальным условием, т.е. начальным условием, отличающимся от (2).

Решение называется устойчивым по Ляпунову решением уравнения (1), если: , решение возмущённой задачи Коши (3) останется в -окрестности при всех : .

Лемма Устойчивость решения уравнения (1) эквивалентна устойчивости нулевого решения соответствующего однородного уравнения:

(6)

док: Обозначим через . Вычитая уравнения и начальные условия для этих функций, получаем, что является решением задачи Коши: 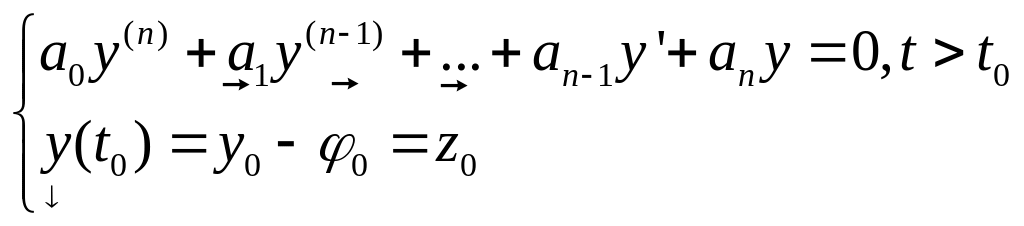(7). Как легко видеть, определение устойчивости решения уравнения (1): в терминологии переписывается в виде , что и является определением устойчивости нулевого решения однородного уравнения (6).

Вывод: при изучении вопросов устойчивости решений линейных ОДУ достаточно ограничиться исследованием устойчивости нулевых решений однородных уравнений.

Устойчивое решение называется асимптотически устойчивым решением уравнения (1), если: , решение возмущённой задачи Коши (3) неограниченно приближается к при : .Вообще говоря, из асимптотической устойчивости не следует просто устойчивость решения.

Лемма(о сведении к асимптотической устойчивости нулевого решения)

Асимптотическая устойчивость решения уравнения (1) эквивалентна асимптотической устойчивости нулевого решения соответствующего однородного уравнения (6).

док: Обозначим через . Вычитая уравнения и начальные условия для этих функций, получаем, что является решением задачи Коши(7). Тогда условие асимптотической устойчивости решения уравнения (1): в терминологии переписывается в виде