11. Функция Грина краевой задачи. Теорема о существовании функции Грина: шаг2(построение функции Грина).
Опр: (1)
(2)
(3)
где и , – заданные функции, причем , , называется функция , удовлетворяющая требованиям:
, где ;
при любом фиксированном и удовлетворяет однородному уравнению (1): при
при любом фиксированном первая производная имеет в точке разрыв первого рода, причём:
при любом фиксированном функция удовлетворяет краевым условиям по x: , .
Теорема о сущ шаг 2
-вронскиан
пары функций
.
Определим
Проверим теперь выполнение условий 1)-4)
, где ; Действительно, знаменатель
и не обращается в нуль, так как
а Вронскиан системы линейно независимых
решений однородного линейного уравнения
всюду отличен от нуля. Числитель же
непрерывен и даже дважды непрерывно
дифференцируем в
.
Однако при
и
при
у него один и тот же предел:
при любом фиксированном и удовлетворяет однородному уравнению (1): при Очевидно так, ибо мы строили и как решения однородного уравнения, а все остальные множители от x вообще не зависят.
при любом фиксированном первая производная имеет в точке разрыв первого рода, причём:
Для того, чтобы убедиться в справедливости этого равенства для по-
строенной , найдём
,
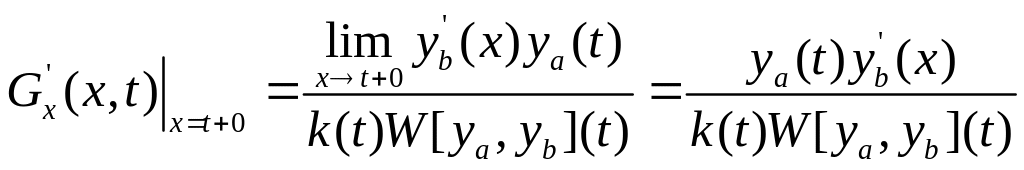откуда
при любом фиксированном функция удовлетворяет краевым условиям по x: ,
При этом при построении функции мы позаботились о том,
чтобы при
она вела себя как
,
а при
– как
.
Поскольку мы строили
и
так,
чтобы
они удовлетворяли КУ, – на левом конце, – на правом, сразу
получается, что
12. Функция Грина краевой задачи. Теорема о единственности функции Грина.
Опр: (1)
(2)
(3)
где и , – заданные функции, причем , , называется функция , удовлетворяющая требованиям:
, где ;
при любом фиксированном и удовлетворяет однородному уравнению (1): при
при любом фиксированном первая производная имеет в точке разрыв первого рода, причём:
при любом фиксированном функция удовлетворяет краевым условиям по x: , .
Теорема:
Пусть
и
– заданные функции,
,
,
и однородная (т.е. при
)
задача (1) –(3) не имеет других решений,
кроме тождественного нуля. Тогда не
может быть двух разных функций Грина
и
краевой
задачи 1-3
док:
Рассмотрим
разность функций Грина
и
:
Так как и – функции Грина одной и той же задачи, их разность обладает следующими свойствами:
,
где
при любом фиксированном
и удовлетворяет однородному уравнению
(1):
при
при любом фиксированном первая производная
непрерывна
в точке
разрыв
первого рода, причём:
=
=
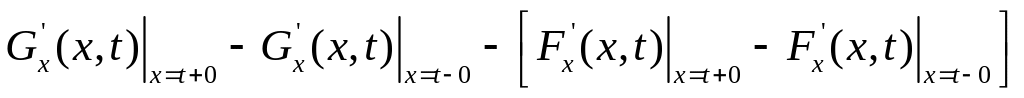при любом фиксированном функция
удовлетворяет
краевым условиям по x:
,
.
Из пункта 2) следует, что:
Тогда в силу пункта 3) получим, что правая часть непрерывна, в том числе
и при x = t, откуда
.Но
в этом случае пункт 2) влечёт, что
удовлетворяет
однородному уравнению (1):
.
Итак, функция
есть
решение однородного уравенения1,
удовлетворяющее однородным КУ (2) – (3).
По условию теоремы это означает, что
,
те
