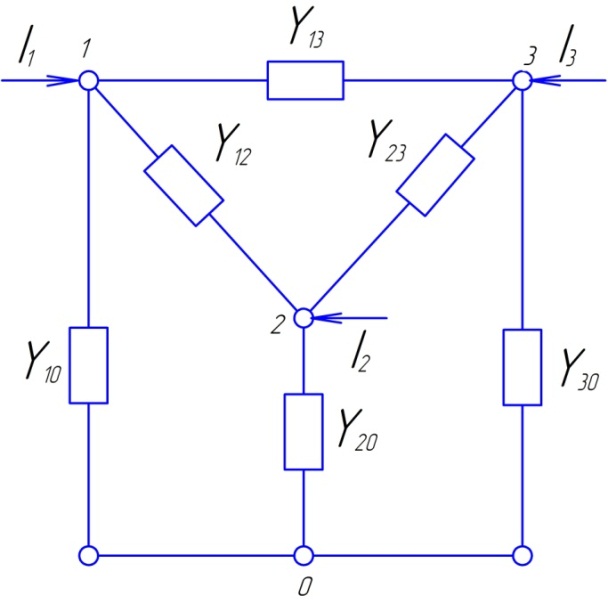
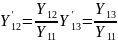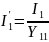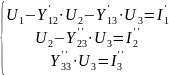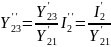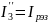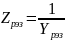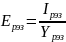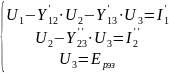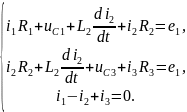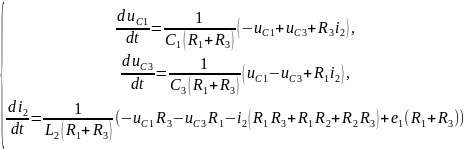- •Абагульненыя раўнанні стану на аснове законаў Кiрхгофа
- •2. Вузлавыя раўнанні
- •Контурныя раўнаннi
- •4 .Пабудаванне 2ой матрыцы злучэнняу па першай.
- •5. Рашыць метадам Гаўса слау:
- •6. Рашыць слау па схеме Жардана:
- •7 Абарачэнне квадратнай матрыцы метадам Гаўса
- •8. Метадам простай iтэрацыi рашыць слау:
- •9 Метад Зэйдэля (метад палепшанай iтерацыі)
- •Метад Зэйдэля (метад палепшанай iтерацыі)
- •11 (Начало в 10)
8. Метадам простай iтэрацыi рашыць слау:

Умовы збежнасцi (22) для кожнага раўнання выконваюцца: для кожнага радка маем 1+1<4. Прыводзiм сiстэму да выгляду, зручнага для выканання iтэрацый:
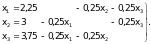 (23)
(23)
У якасцi пачатковага наблiжэння возьмем матрыцу C:

Першае наблiжэнне X(1) атрымаем, падставiўшы X(0) у правую частку сiстэмы (23):
 .
.
Такiм чынам, першае наблiжэнне:
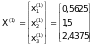 .
.
Падстаўляем яго ў правую частку сiстэмы (23) i вылiчваем другое наблiжэнне:
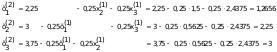
Або:

Прымяняючы гэты алгарытм, атрымаем наступныя наблiжэннi:
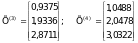
i так далей.
Дакладнае рашэнне сiстэмы:
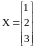
9 Метад Зэйдэля (метад палепшанай iтерацыі)
Метад Зэйдэля (метад палепшанай iтерацыі)
Метад
Зэйдэля адрознiваецца ад метада простай
iтэрацыi тым, што пры разлiку невядомай
велiчынi
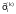 k-ага наблiжэння ў правую частку сiстэмы
(23) падстаўляюцца пераменныя
k-ага наблiжэння ў правую частку сiстэмы
(23) падстаўляюцца пераменныя
 k-ага наблiжэння, якiя ўжо вылiчаны на
бягучым k-тым iтэрацыйным кроку з першага,
другога, ... і-1 раунанняў , i пераменныя
k-ага наблiжэння, якiя ўжо вылiчаны на
бягучым k-тым iтэрацыйным кроку з першага,
другога, ... і-1 раунанняў , i пераменныя
 k-1-ага наблiжэння, атрыманыя на папярэднiм
iтэрацыйным кроку. Напрыклад, формулы
для разлiку першага наблiжэння X(1)
ў разгорнутай форме для сiстэмы трэцяга
парадку маюць выгляд:
k-1-ага наблiжэння, атрыманыя на папярэднiм
iтэрацыйным кроку. Напрыклад, формулы
для разлiку першага наблiжэння X(1)
ў разгорнутай форме для сiстэмы трэцяга
парадку маюць выгляд:
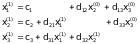
У большасцi выпадкаў метад Зэйдэля дае лепшую збежнасць iтэрацыйнага працэсу ў параўнаннi з метадам простай iтэрацыi.
Прыклад 5. Рашыць сiстэму прыкладу 4 метадам Зэйдэля.
Выкарыстоўваючы сiстэму (23) i нулявое наблiжэнне X(0)=C, атрымаем першае наблiжэнне X(1):

Прымяняючы паслядоўна алгарытм Зэйдэля, атрымаем:
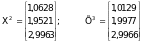
i так далей.
Параўноўваючы атрыманыя рэзультаты з дакладным рашэннем сiстэмы i з рэзультатамi метаду простай iтэрацыi, можна канстатаваць лепшую збежнасць метаду Зэйдэля ў параўнаннi з метадам простай iтэрцыi.
11 (Начало в 10)
Uya вместо U
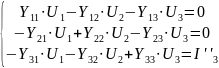
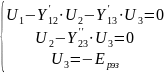
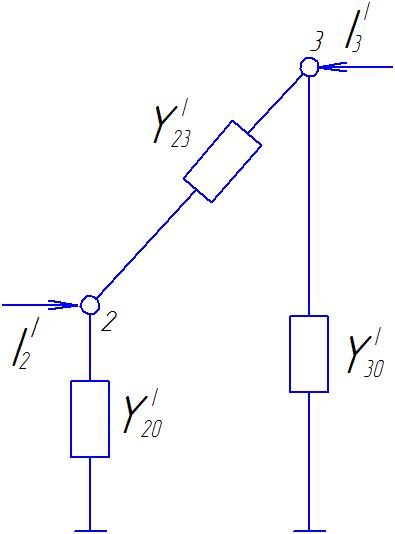
Uуа3= –9,035 В;
Uуа2=y23Uуа3=0,8( –9,035)= –7,228 В;
Uуа1=y12Uуа2+y13Uуа3=0,2( –7,228)+0,4( –9,035)= –5,0596.В.
Теперь выполним наложение собственно аварийного режима на доаварийный в соответствии с формулой Uва =Uв+Uвуа и получим узловые напряжения аварийного режима:
Uа3=U3+Uуа3=9,035+(-9,035)=0 В;
Uа2=U2+Uуа2=7,895+(-7,228)=0,667 В;
Uа1=U1+Uуа1=7,193+(-5,0596)=2,1334 В;
По узловым напряжениям для аварийного режима рассчитаем токи в ветвях схемы (положительное направление - от узла с большим номером к узлу с меньшим номером):
Iа10=(Uа1 –Uа0 –Е10)/Z1,0=(2,1334-0-5)/0,5=-5,7332 A;
…
Iа31=(Uа3 –Uа1)/Z31=(0 –2,1334/0,5=-4,2668 A.
В качестве контроля результатов отметим Iа3,0 +Iа3,1 +Iа32=I3
10 Электрычная інтэрпрытацыя Метада Гаўса
|
|
|
|
|
j-номер удаленного узла n и k – номера узлов, соед. с узлом j |
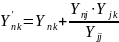

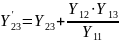
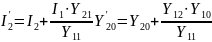
12
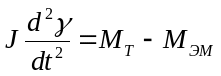
Дз е J – момант инерцыи ротару+ момант инерцыи турбины(кали яна падключана)
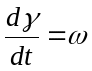 - хуткасць вярчэння
ротара
- хуткасць вярчэння
ротара
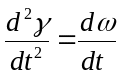 -
вуглавое паскарэнне ротара
-
вуглавое паскарэнне ротара
Таким чынам палучим систэму ДУ першага парадку:
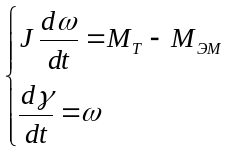
13 (2
катушки)

 Для
таго, каб прывесці сістэму дыферэнцыяльных
раунанняў да нармальнага віда зробім
наступнае:
Для таго, каб атрымаць
Для
таго, каб прывесці сістэму дыферэнцыяльных
раунанняў да нармальнага віда зробім
наступнае:
Для таго, каб атрымаць
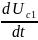 падставім замест
падставім замест
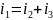 у чацьвёртае раўнанне сістэмы і выразім
патрэбную велічыню:
у чацьвёртае раўнанне сістэмы і выразім
патрэбную велічыню:
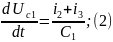
Выразім
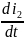 із першага раунання сістэмы (1):
із першага раунання сістэмы (1): 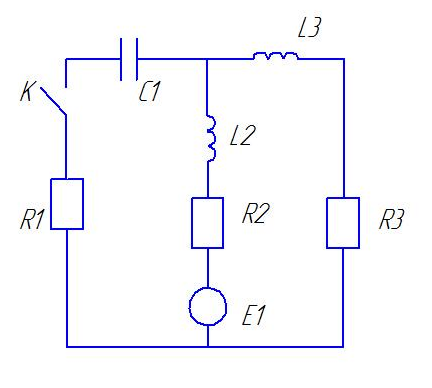


Выразім
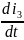 з другога раўнання сістэмы (1):
з другога раўнання сістэмы (1):

з улікам таго ,што
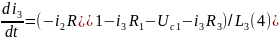
Сістэму дыферэнцыйных раўнанняў складзём з раўнанняў (2), (3), (4):
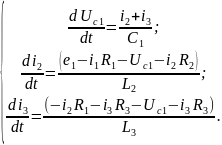
13 (2 конденсатора)
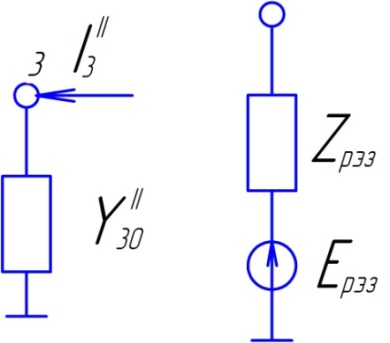
П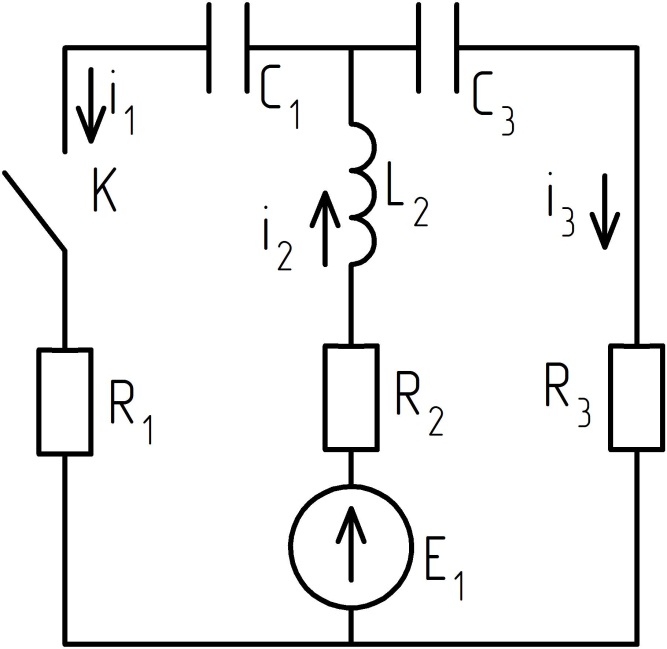 асля
замыкання ключа ў схеме атрымоўваецца
два лінейна незалежных контура і адзін
лінейна незалежны вузел. Дынаміка
пераходнага рэжыму электрычнай сістэмы
абумоўлена існаваннем ў ёй рэактыўных
элементаў: індуктыўнасці L
і кандэнсатараў C.
Іх колькасць апрадзяляе парадак сістэмы
дыферанцыяьных раўнанняў.
асля
замыкання ключа ў схеме атрымоўваецца
два лінейна незалежных контура і адзін
лінейна незалежны вузел. Дынаміка
пераходнага рэжыму электрычнай сістэмы
абумоўлена існаваннем ў ёй рэактыўных
элементаў: індуктыўнасці L
і кандэнсатараў C.
Іх колькасць апрадзяляе парадак сістэмы
дыферанцыяьных раўнанняў.
Саставім сістэму раўнанняў па законам Кірхгофа
|
(1) |
Гэтая сістыма не з’яўляецца замкнутай, пагэтаму неабходна дапоўніць яе яшчэ двума раўнаннямі:

Трэба
прывесци систэму ДУ да кананичнага
выгляду:
 ,
таму што да такой формы написаны праграмы
ликавага рашэння ДУ.
Сістэма
дыферэнцыяльных
раўнанняў
(2), зведзеная
да
нармальнага(кананічнай)
стану,
наступная:
,
таму што да такой формы написаны праграмы
ликавага рашэння ДУ.
Сістэма
дыферэнцыяльных
раўнанняў
(2), зведзеная
да
нармальнага(кананічнай)
стану,
наступная:
|
14
Пример.
Решить методом Эйлера дифференциальное
уравнение
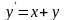 при начальном условии у(0) = 1 на отрезке
[0; 0,5] с шагом 0,1.
при начальном условии у(0) = 1 на отрезке
[0; 0,5] с шагом 0,1.
Применяем
формулу
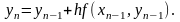
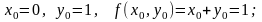





Производя аналогичные вычисления далее, получаем таблицу значений:
i |
0 |
1 |
2 |
3 |
4 |
5 |
xi |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
yi |
1 |
1,1 |
1,22 |
1,362 |
1,528 |
1,721 |
15 Пример. Решить методом Рунге – Кутта дифференциальное уравнение при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
Для i = 0 вычислим коэффициенты ki.

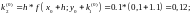

Последующие вычисления приводить не будем, а результаты представим в виде таблицы.
i |
xi |
k |
yi |
yi |
|
0
|
0 |
1 |
0,1000 |
0,1100 |
1 |
2 |
0,1200 |
||||
1 |
0,1 |
1 |
0,1210 |
0,1321 |
1,1100 |
2 |
0,1431 |
||||
2 |
0,2 |
1 |
0,1442 |
0,1564 |
1,2421 |
2 |
0,1686 |
||||
3 |
0.3 |
1 |
0,1699 |
0,1834 |
1,3985 |
2 |
0,1968 |
||||
4 |
0,4 |
1 |
0,1982 |
0,2131 |
1,5819 |
2 |
0,2280 |
||||
5 |
0,5 |
|
1,795 |
||
16 Пример. Решить методом Рунге – Кутта дифференциальное уравнение при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.
Для i = 0 вычислим коэффициенты ki.
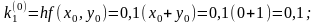
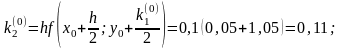
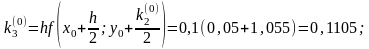
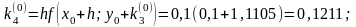

Последующие вычисления приводить не будем, а результаты представим в виде таблицы.
i |
xi |
k |
yi |
yi |
|
0
|
0 |
1 |
0,1000 |
0,1104 |
1 |
2 |
0,1100 |
||||
3 |
0,1105 |
||||
4 |
0,1155 |
||||
1 |
0,1 |
1 |
0,1210 |
0,1325 |
1,1104 |
2 |
0,1321 |
||||
3 |
0,1326 |
||||
4 |
0,1443 |
||||
2 |
0,2 |
1 |
0,1443 |
0,1569 |
1,2429 |
2 |
0,1565 |
||||
3 |
0,1571 |
||||
4 |
0,1700 |
||||
3 |
0.3 |
1 |
0,1700 |
0,1840 |
1,3998 |
2 |
0,1835 |
||||
3 |
0,1842 |
||||
4 |
0,1984 |
||||
4 |
0,4 |
1 |
0,1984 |
0,2138 |
1,5838 |
2 |
0,2133 |
||||
3 |
0,2140 |
||||
4 |
0,2298 |
||||
5 |
0,5 |
|
1,7976 |
||