1. Абагульненыя раўнанні стану на аснове законаў Кiрхгофа

Абагульненае раўнанне стану электрычнага ланцуга на аснове законаў Кiрхгофа мае выгляд [1]:

AI=F; (1)

дзе 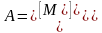- квадратная матрыца mm, дзе m - колькасць галін электрычнай схемы;

M - першая матрыца злучэнняў (інцыдэнцый), або вузлавая матрыца, памерам (n-1)m, дзе n - колькасць усіх вузлоў схемы, а (n-1) - колькасць лінейна незалежных вузлоў схемы;

N - другая матрыца злучэнняў (інцыдэнцый), або контурная матрыца, памерам km, дзе k - колькасць лінейна незалежных контураў схемы;

Z - дыяганальная матрыца супраціўленняў галін схемы памерам mm;

I- матрыца - слупок токаў у галінах схемы памерам m1;

- матрыца - слупок правых частак абагульненага раўнання памерам m1;

J - матрыца - слупок токаў крыніц тока ў незалежных вузлах схемы памерам (n-1)1;

Е_к - матрыца - слупок контурных электрарухаючых сіл (ЭРС) ў лінейна незалежных контурах памерам k1.

Першая матрыца злучэнняў М паказвае, як падключана j-тая галіна схемы да і-тага вузла: пачаткам (элемент m_ij матрыцы М роўны адзінцы), канцом (m_ij=-1) або не падключана зусім (m_ij=0). Вузел з нулявым нумарам выбіраем у якасці базіснага, ён з’яўляецца лінейна залежным вузлом, і для яго адпаведны радок у матрыцы М не запісваецца. Нумары супраціўленняў і крыніц у схеме адпавядаюць нумарам галін. Для схемы на мал.1 матрыца М мае выгляд:

Элементы n_ij матрыцы N паказваюць, ці ўваходзіць j-ая галіна схемы ў і-ы контур (n_ij=0, калі j-ая галіна ў і-ы контур не ўваходзіць) і ці супадае накірунак j-ай галіны з накірунам і-тага контура (n_іj=1 - cупадае; n_іj=-1 - не супадае):

Дыяганальная матрыца супраціўленняў галін схемы Z утрымлівае на галоўнай дыяганалі супраціўленні схемы, а недыяганальныя яе элементы роўны нулю:

2. Вузлавыя раўнанні

Вузлавыя раўнанні звязваюць невядомыя вузлавыя напружанні з зададзенымі параметрамі схемы і зададзенымі параметрамі рэжыму схемы. Сістэма вузлавых раўнанняў у матрычнай форме мае выгляд [1,2]:

Y_вU_в=J-MY_вЕ.

Калі ўсе крыніцы электрычнай схемы прадставіць ў выглядзе крыніц тока (матрыца ЭРС галін схемы Е=0), то сістэма раўнанняў для вузлавых напружаняў спрашчаецца:

Y_вU_в=J (3),

дзе Y_в - матрыца вузлавых праводнасцей схемы памерам (n-1)(n-1) (n-колькасць вузлоў схемы); элемент y_ii матрыцы Y_в, які знаходзіцца ў і-ым радку на галоўнай дыяганалі, роўны суме праводнасцей галін, падключаных да і-ага вузла схемы (уласная праводнасць і-ага вузла); элемент y_ij на перакрыжаванні і-тага радка і j-ага слупка матрыцы Y_в роўны ўзятай са знакам мінус праводнасці галіны, уключанай паміж i-ым і j-ым вузламі схемы (узаемная праводнасць паміж i-ым і j-ым вузламі);

Токі ў галінах схемы ў мадэлі (3) на аснове вызлавых раўнанняў пры вядомых вузлавых напружаннях U_В можна разлічыць па наступных формулах, улічваючы, што вузлавое напружанне u_В0 нулявога вузла прынята роўным нулю:

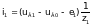
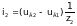
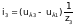
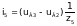
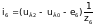(7)

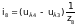
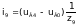
3. Контурныя раўнаннi

Контурныя раўнаннi ў матрычнай форме маюць выгляд [1,2]:

.

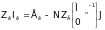Для схемы, у якой усе крынiцы электрычнай энергii прадстаўлены крынiцамi ЭРС (матрыца токаў крыніц тока J=0), гэтыя раўнанні спрашчаюцца:

Z_кI_к=Е_к (5)

дзе: Z_к - матрыца контурных супраціўленняў:

,

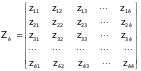якая мае парадак к (колькасць лінейна незалежных контураў схемы). Дыяганальны элемент z_ii гэтай матрыцы роўны суме супраціўленняў галін, якія ўваходзяць у i-ты контур. Недыяганальны элемент z_ij роўны суме супраціўленняў галін, якія ўваходзяць адначасова ў i-ты і ў j-ты контуры, прычым сума мае знак плюс, калі накірункі і-тага і j-тага контураў у гэтых галінах супадаюць, і знак мінус,. калі не супадаюць.

Токі ў мадэлі (5) на аснове контурных раўнанняў ў галінах 5, 6, 7, 8, 9, якія з’яўляюцца хордамі, ёсць контурныя токі і_к1, і_к2, і_к3, і_к4, і_к5:

і₅=і_к1; і₆=і_к2; і₇=і_к3; і₈=і_к4; і₉=і_к5. (8а)

Токі ў галінах 1, 2, 3, 4, якія ўваходзяць ў дрэва, можна разлічыць па формулах:

і₁=-і_к2-і_к3-і_к5; і₂=і_к1-i_к2-і_к4-і_к5;

і₃=-і_к1-і_к3+і_к4; і₄=-і_к4-і_к5.