19

Федеральное агентство по образованию и науке

Рязанский государственный радиотехнический университет

Кафедра ТОР

5110

Учебное пособие

по курсу:

Теория электрической связи.

Рязань 2010

Настоящее пособие является продолжением серии изданий для подготовки студентов специальности 2012 «Средства связи с подвижными объектами» к сдаче государственного экзамена. Включает себя основные теоретические сведения по предмету: «Теория электрической связи».

2. Спектральный анализ непериодических сигналов. Прямоугольный видео и радиоимпульсы. 5

3,4. Преобразование спектров сигналов в нелинейных устройствах. Комбинационные частоты. 7

5. Дискретное представление непрерывных сигналов. 8

6. Преобразование частоты радиосигналов 9

7. Амплитудный детектор радиосигналов 10

8. Амплитудная модуляция ВЧ колебаний 11

9. Критерии качества и правила приема дискретных сообщений. 12

10. Когерентный прием сигналов. 13

11. Согласованные и квазиоптимальные фильтры. 14

12. Вероятность ошибочного приема точно известных сигналов. 15

13. Количество информации, энтропия, избыточность источника сообщений. 17

1. Спектральный анализ периодических сигналов. Сигналы с АМ, БМ.

Спектральное представление периодического сигнала s(t) находится разложением сигнала в ряд Фурье.

Тригонометрическая форма ряда Фурье:

где – основная частота периодического сигнала;

Т – период сигнала;

– постоянная составляющая.

n-я гармоника сигнала:

где , . С учетом этого,

Сигнал с амплитудной модуляцией при модулирующем сигнале

где А₀ – уровень немодулированной несущей;

М – коэффициент модуляции;

модулирующая частота;

фаза огибающей;

_несущая частота;

_фаза несущего колебания.

Временная диаграмма:

Спектральные диаграммы:

Амплитудная

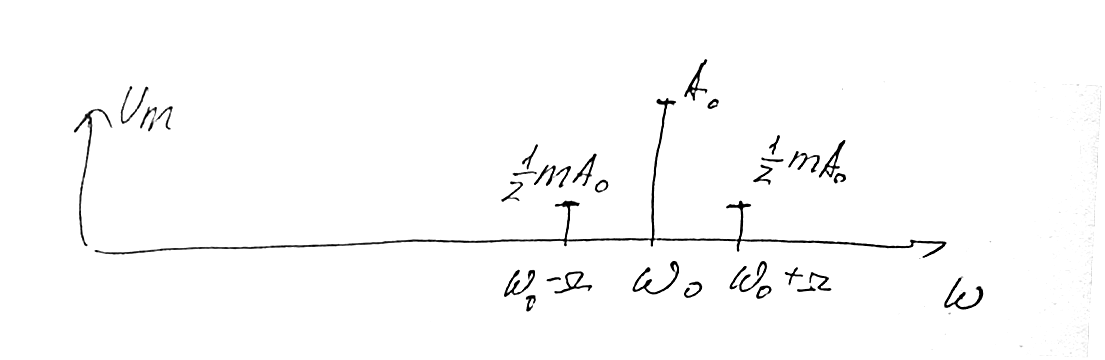Δω=2Ω

Фазовая

Спектр периодического сигнала – линейчатый.

Сигнал с балансной амплитудной модуляцией.

Сигнал с БМ не содержит несущего колебания. БМ энергетически более выгодна.

Спектр:

Временная диаграмма:

Огибающая не совпадает по форме с первичным сигналом.

2. Спектральный анализ непериодических сигналов. Прямоугольный видео и радиоимпульсы.

Спектральным представлением непериодического сигнала s(t) является его спектральная плотность S(ω). Спектральная плотность и сигнал связаны прямым и обратным преобразованиями Фурье:

- прямое

- обратное

Распишем S(ω):

Модуль S(ω):

– АЧХ спектра или амплитудный спектр.

– ФЧХ спектра или фазовый спектр.

Прямоугольный импульс:

Спектральная плотность:

Спектральные диаграммы

Спектр непериодического сигнала – сплошной.

Ширина спектра по первому нулю огибающей:

.

Радиоимпульс:

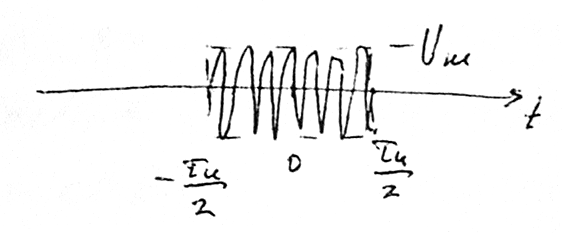
Спектральная плотность:

Спектр радиоимпульса соответствует спектру видеоимпульса, перенесенному в окрестности центральных частот ±₀.

Значение максимумов уменьшилось вдвое, ширина спектра увеличилась в 2 раза.

3,4. Преобразование спектров сигналов в нелинейных устройствах. Комбинационные частоты.

В отклике нелинейного устройства на входные воздействия может быть достаточно много спектральных составляющих. Одни являются полезными, другие вызывают искажения. Полезные составляющие спектра выделяют для дальнейшего использования, мешающие – подавляют.

Рассмотрим преобразование спектра сигнала при бигармоническом воздействии на нелинейный элемент.

Бигармоническое напряжение:

Считаем характеристику НЭ полиномиальной,

Положим n=3, подставим u(t) и представим ток НЭ в виде суммы гармоник с различными частотами:

Из соотношения видно, что ток содержит три группы составляющих:

- гармоники с частотой k₁₁ и начальными фазами k₁₁, k₁=1, 2,…, n;

- гармоники с частотой k₂₂ и начальными фазами k₂₂, k₂=1, 2,…, n;

- комбинационные составляющие с частотами k₁₁± k₂₂ и начальными фазами k₁₁ ± k₂₂ , где |k₁| + |k₂| = 2, 3, … , k₁ и k₂ – отличные от нуля целые числа любого знака.

Комбинационные частоты возникают в нелинейных цепях только при одновременном воздействии двух или большего числа гармонических колебаний.

В данном случае комбинационные частоты ₁±₂, 2₁±₂, ₁±2₂.

Спектр тока для рассматриваемого случая:

Комбинационные частоты используются при преобразовании частоты, модуляции, синхронном детектировании.