1. Предмет теории вероятностей, два признака случайного явления, постулат теории вероятностей. Примеры построения пространств элементарных исходов.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

Признаки случайного явления:

• отсутствие детерминированности (однозначная предопределённость)

• статистическая закономерность

Постулат ТВ:

Случайное явление характеризуется числом рє[0;1]

P(Ѡ1)=P(Ѡ2)=...=P(Ѡn)=1/n, где Ѡ – элементарный исход, n - число опытов.

Пример: подбрасываем 2 монеты по 2 раза, возможные исходы:

• Ѡ1={орел,орел}

• Ѡ2={орел,решка}

• Ѡ3={решка,решка}

• Ѡ4={решка,орел} (случай с ребром не рассматриваем)

Вероятность для каждого события равна = ¼.

13. Определение условной вероятности, ее свойства.

Определение. Условной вероятностью события А при условии, что наступило событие В, называется отношение числа k тех благоприятствующих А исходов, которые и благоприятствуют В, к числу m всех исходов, благоприятствующих В.

Условная вероятность обозначается: P(A/B). По определению:если В - невозможное событие P(A/B)=k/m, то не определена P(A/B)

Свойства условных вероятностей:

• Всегда 0 ≤ P(A/B) ≤1, причем P(A/B) =0 , если АВ - невозможное событие, и P(A/B)=1, если (А включено в В).

• Есл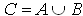и и 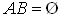, то для любого события D .

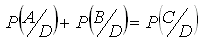• Если 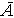событие, противоположное A, то .

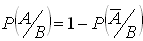19. Схема Бернулли: традиционная постановка задачи и построение вероятностного пространства.

Схемой Бернулли или последовательностью независимых одинаковых испытаний с двумя исходами называется случайный эксперимент, в котором:

• Проводится независимых испытаний;

• каждое испытание кончается одним из двух исходов (один исход называется ’’успех” и обозначается 1, а второй - ’’неуспех” и обозначается 0);

• вероятность появления ’’успеха” одна и та же в каждом испытании и равна .

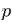Числа и называются параметрами схемы Бернулли. Формальное описание модели такого эксперимента дано в следующем определении.

Пример:

Выпадение герба будем считать ’’успехом”. Это схема Бернулли с параметрами

Обычно в рамках схемы Бернулли мы хотим вычислить вероятность не отдельного элементарного исхода, а некоторого более сложного события. Например, в предыдущем примере нас может интересовать вероятность того, что выпало ровно 3 герба. Такой вопрос является наиболее типичным для схемы Бернулли. Пусть есть событие, состоящее в том, что в независимых испытаниях мы получили ровно успехов. По определению вероятности события , где мы воспользовались тем, что вероятности элементарных исходов в все одинаковые и вычисляются по формуле (3), а число различных исходов равно размещению единиц по n мест без учета порядка.

19. Схема Бернулли. Локальная и интегральная предельные теоремы Муавра – Лапласа. Неравенство Берри – Эссена.

Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают , а непоявления (неудачи) его . Бернулли установил, что вероятность ровно успехов в серии из повторных независимых испытаний вычисляется по следующей формуле:

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из k событий с вероятностью ( ( . Вероятность появления раз первого события и - второго и -го находится по формуле:

Локальная и интегральная предельные теоремы Муавра – Лапласа:

Неравенство Берри — Эссеена — неравенство, позволяющее оценить скорость сходимости суммы независимых случайных величин к случайной величине с нормальным распределением.

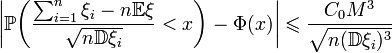, где константа Берри-Эссеена

Для выполнения неравенства Берри-Эссеена необходимо существование третьего центрального момента.

Если потребовать только , скорость сходимости будет сколь угодно медленная.

Если потребовать , скорость сходимости не увеличится.