1. Понятие информации. Примеры , определения.

Слово «Информация» происходит от латинского слова informatio – сведение, разъяснение, ознакомление. Строгого научного определения информации в настоящее время не существует, принято оперировать понятием об информации, которое рассматривается как базовое понятие и его невозможно определить через другие, более простые понятия. Содержание базовых понятий выясняется на примерах или путем сопоставления с другими понятиями.

Имеется несколько сотен определений понятия информации. Среди них, например, такие

информация есть отражение различных сторон реального мира,

информация- это продукт взаимодействия данных и адекватных им методов,

информация – есть снятая неопределенность, результат выбора из возможных альтернатив,

информация – это длина алгоритма, позволяющего преобразовать один объект в другой, т.е. мера сложности объекта и т.д.

2. Аттрибутивные свойства информации. Примеры.

Атрибутивные свойства – это свойства, без которых информация не существует. К ним относятся:

1. Непрерывность. Информация имеет свойство сливаться с уже накопленной ранее, тем самым, способствуя ее дальнейшему накоплению.

2. Дискретность. Содержащиеся в информации сведения, знания дискретны, т.е. характеризуют отдельные фактические данные и свойства изучаемых объектов, которые распространяются в виде различных сообщений, состоящих из букв, цифр, знаков, цвета, линий.

3. Неотрывность от физического носителя.

4. Языковая природа информации.

Рассматривая последние два свойства надо учитывать, что жесткой связи информации с конкретным носителем или с конкретным языком нет.

3. Прагматические свойства информации.

Прагматические свойства – характеризуют степень полезности информации для потребителя. К ним относятся:

1. Новизна

2. Полезность

3. Ценность

4. Объективность и субъективность (относительность понятия объективности).

5. Полнота

6. Достоверность

7. Адекватность

8. Доступность

9. Актуальность

1. Операции, выполняемые с информацией.

Если рассматривать информатику как техническую науку, занимающуюся способами создания, хранения, воспроизведения, обработки и передачи данных (информации) средствами вычислительной техники, принципами функционирования этих средств и методами управления ими.

Операции с данными:

• сбор данных;

• формализация данных;

• фильтрация данных;

• сортировка данных;

• архивация данных;

• защита данных;

• транспортировка данных;

• преобразование данных.

Данные и информация, грубо говоря, связаны следующим образом: информация – это полезное содержание данных, данные – это форма представления информация. Можно сказать, что данные представляют собой информацию в синтаксическом аспекте(Синтаксический аспект затрагивает форму представления информации, но не ее смысловое содержание).

5. Фундаментальные и технические науки, относящиеся к информатике.

*Теоретическая информатика

*Практическая информатика

*Техническая информатика

*Прикладная информатика

*Естественная информатика

Информатизация общества в части материально-технической базы, математического и программного обеспечения информационных технологий изобилует различными науками: кибернетикой, системотехникой, теорией информации, а в формирования функциональных подсистем – различными общественными науками: экономикой, правоведением, психологией. В формировании информационных участвуют и науки, относящиеся к той или иной автоматизируемой области: когда речь идет о внедрении ЭВМ в здравоохранение; педагогика (компьютеризация учебного процесса); военные науки (использование ЭВМ в военном деле), экономика т.д. Каждая из указанных наук рассматривает компьютеризацию со своей стороны, прилагает к ней свои законы и принципы. Информационная реальность включает в себя физиче­ские, математические, химические, биологические, социальные, тех­нические и другие знания, а также материальные ценности, создан­ные человеком, включая и технологию получения

6. Алгебра логики. Какой смысл в алгебре логики имеют понятия константа, переменная, операция, формула, функция?

Алгебра логики – раздел математики, изучающий процессы умозаключений и законы, которые позволяют из истинности одних высказываний делать заключения об истинности или ложности других высказываний, независимо от их конкретного содержания. Алгебра логики (булева алгебра) была создана в 1854 г. Дж. Булем и в настоящее время находит широкое применение при разработке алгоритмов и для структурно-функционального описания, анализа и синтеза современных электронных схем.

* Константы- логический ноль(0) и логическая единица(1)

*Логическая переменная- переменная, значением которой может быть любое высказывание (Высказывание – повествовательное предложение, относительно которого определенно и объективно можно сказать истинно оно или ложно (ЛОЖЬ или ИСТИНА, 0 или 1, TRUE или FALSE)).

*Базовыми операциями алгебры логики служат операции логического умножения – конъюнкции , логического сложения – дизъюнкции, логического отрицания – инверсии .

*Логическая функция - это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции.

Из элементарных высказываний с помощью логических связок " и", "или", "не", "если : то" и других (логических операций) строятся сложные высказывания - формулы (или функции )алгебры логики.

*Определение логической формулы:

1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.

2. Если А и В — формулы, то , А . В , А v В , А B , А В — формулы.

3. Никаких других формул в алгебре логики нет

Вводятся алгебраич. операции над высказываниями: конъюнкция A·B (читается «А и В», другие обозначения: AB, A&B, А⋀В; другие названия: логическое умножение, булево умножение), дизъюнкция А⋁В («читается А или В»; другое обозначение: А+В; другие названия: логическое сложение, булево сложение), импликация А→В (читается: «Если А, то В» или «А влечет В», или «Aимплицирует В», или «Из А следует В»; другое обозначение: A⊃B; другое название: логическое следование), эквиваленция А~В (читается: «А эквивалентно B» или «А равнозначно В», или «А,если и только если В»: другие обозначения: А≡В, А↔В; другие названия: эквивалентность, равнозначность, равносильность), отрицание А (читается: «не А», или «А ложно», или «неверно, чтоА», или «отрицание А»; другие обозначения: ¬А, ~А, A´; другое название: инверсия), а также иногда и другие операции.

7. В чём смысл терминов «вычисление формулы» и «преобразование формулы», Примеры.

Основные объекты алгебры арифметики - выражения (формулы), состоящие из букв, знаков операций и скобок. С формулами производят процедуры двух типов: вычисления и преобразования.     Вычисления - вместо букв подставляют числа, знаки указывают действия, а скобки их порядок. Каждая формула задает функцию. Переменные - буквы формулы. Логические формулы определяют, выражение истинно или ложно, и таким образом, вычисление логической формулы заканчивается получением оценки "Истина" или "Ложь"

  Преобразование формулы происходит так: исходная формула или ее часть F₁ заменяется другой, в результате получается новая формула F₂, которая эквивалентна F₁ (т.е. при любых значениях аргументов F₁ и F₂ дают один и тот же результат). Преобразование выражений производится на основе законов арифметики, а также полученных из них соотношений. По аналогии строится алгебра логики. Она рассматривает логические выражения как алгебраические, которые можно преобразовать по определенным правилам. Разница заключается в том, что в выражениях алгебры логики переменные являются логическими (0 и 1). Знаки операций обозначают логические операции (логические связки).  Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры 

8)Приведите таблицы функций конъюнкция, дизъюнкция, равнозначность, неравнозначность, штрих Шеффера, стрелка Пирса, отрицание. Какие знаки операций используют для этих функций в формулах?

Базовыми операциями алгебры логики служат операции логического умножения – конъюнкции (обозначается точкой или знаком ), логического сложения – дизъюнкции (обозначается знакам + или ), логического отрицания – инверсии (обозначается надчеркиванием или знаком ). При составлении формул применяются скобки, чтобы изменять порядок выполнения операций. Наивысшим приоритетом обладает операция инверсии, затем идет конъюнкция и потом уже дизъюнкция.

Таблицы истинности для указанных операций:

Штрих Шеффера ("И - НЕ")

Стрелка Пирса ("ИЛИ - НЕ")

9) Как построить таблицу функции по формуле?

Таблица функции для сложного выражения строится по следующему алгоритму:

1. Определяется количество строк по формуле

количество строк = 2^n + строка для заголовка, где n – количество простых высказываний,

2. Определяется количество столбцов по формуле

количество столбцов = количество переменных + количество логических операций,

3. Строится таблица и заполняется результатами операций в вышеуказанной последовательности, при этом используется таблица истинности простых логических операций

10)Как по таблице функции построить СДНФ?

Совершенная дизъюнктивная нормальная форма булевой функции .   Совершенная дизъюнктивная нормальная форма (СДНФ) относится к числу канонических форм представления функций. Любая булева функция представима в СДНФ (кроме константы 0). Запись произвольной булевой функции в этих формах проста и удобна для последующих преобразований. СДНФ у каждой функции единственны.  СДНФ функции есть дизъюнкция всех ее конституент единицы.  

Алгоритм построения СДНФ по таблице истинности

Дана таблица истинности некоторой функции. Для построения СДНФ необходимо выполнить следующую последовательность шагов:

*Выбрать все строки таблицы, в которых функция принимает значение 1.

*Каждой такой строке поставить в соответствие конъюнкцию всех аргументов или их инверсий (минтерм). При этом аргумент, принимающий значение 0, входит в минтерм с отрицанием, а значение 1 – без отрицания.

*Наконец, образуем дизъюнкцию всех полученных минтермов. Количество минтермов должно совпадать с количеством единиц логической функции.

11)Как построить тупиковую ДНФ?

Пусть f(x1, … , xn) есть некоторая функция алгебры логики. Построим для f некоторую КНФ. Осуществим далее следующие преобразования.

*. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание. В результате получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ.

*. В полученном выражении удалим нулевые дизъюнктивные слагаемые.

*. В полученном выражении проведем все поглощения, а затем удалим дублирующие члены.

В результате проведенных операций получим сокращенную ДНФ функции f.

Определение. Тупиковой ДНФ (ТДНФ) функции f называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции f.

Теорема. Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ.

Для получения МДНФ функции f необходимо построить все ТДНФ функции f и выбрать те из них, которые содержат минимальное число букв.

Алгоритм построения всех тупиковых ДНФ.

Пусть f(x1, x2, …, xn) есть булева функция.

Шаг 1. Построим СДНФ функции f и пусть P1, P2, …,Pn есть ее конституенты (единицы).

Шаг 2. Построим  сокращенную ДНФ функции f и пусть К1, К2, …, Кm – ее простые импликанты.

Шаг 3. Построим матрицу покрытий простых импликант функции f ее коституентами единицы (табл. 34), полагая, что

Таблица 34

N	P1	P2	…	Pj	…	Pn
K1	a11	a12	…	a1j	…	a1n
K2	a21	a22	…	a2j	…	a2n
Ki	ai1	ai2	…	aij	…	ain
Km	am1	am2	…	amj	…	amn

Шаг 4. Для каждого столбца j (1 Ј j Ј n)найдем множество Ej всех тех номеров i строк, для которых aij=1.  Пусть   Составим выражение  Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …, m и с операциями конъюнкции и дизъюнкции.

Шаг 5. В выражении А раскроем скобки приведя выражение А к равносильному выражению  , где перечислены все конъюнкции   элементы ei1, ei2, …, ein которой взяты из скобок 1, 2, …, n соответственно в выражении А.

Шаг 6. В выражении В проведем все операции удаления дублирующих членов и все операции поглощения. В результате получим равносильное выражение С, представляющее собой дизъюнкцию элементарных конъюнкций.

12)Какие законы используют при преобразовании формул?

Приведем основные логические законы (тождественно истинные высказывания), которые позволяют упрощать формулы, заменяя их подформулы эквивалентными выражениями:

Переместительный (коммутативный) закон:

◦ для логического сложения: А Ú B = B Ú A;

◦ для логического умножения: A & B = B & A.

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

Сочетательный (ассоциативный) закон:

◦ для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);

◦ для логического умножения: (A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

Распределительный (дистрибутивный) закон:

◦ для логического сложения: (А Ú B) & C = (A & C) Ú (B & C);

◦ для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C).

Закон определяет правило выноса общего высказывания за скобку.

Закон общей инверсии (законы де Моргана):

◦ для логического сложения: = &;

◦ для логического умножения: = Ú

Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):

◦ для логического сложения: А Ú A = A;

◦ для логического умножения: A & A = A .

Закон означает отсутствие показателей степени.

Законы исключения констант:

◦ для логического сложения: А Ú 1 = 1, А Ú 0 = A;

◦ для логического умножения: A & 1 = A, A & 0 = 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

Закон поглощения:

◦ для логического сложения: А Ú (A & B) = A;

◦ для логического умножения: A & (A Ú B) = A

  А¬А=Л (закон противоречия);

A⋁¬A=И (закон исключенного третьего).

Основная суть алгебры логики как системы методов состоит в использовании преобразований высказываний на основе алгебраических законов, которые имеют место для операций над высказываниями. Эти законы чаще всего имеют вид тождеств, т.е. равенств, верных при всех значениях переменных. Важную роль играют тождества:

Эти тождества, устанавливаемые, напр., с помощью таблиц, позволяют получать другие тождества. Тождеств I–VI достаточно для того, чтобы из них по методу тождественных преобразований можно было вывести всякое (верное, конечно) тождество, левая и правая части которого – выражения алгебры логики, состоящие из переменных А, В, .., констант И, Л и знаков «·», «ν» «–» (не обязательно включая все из них). Добавление же тождеств VII A→B=¬A⋁B, A~B=AB⋁¬A¬B дает возможность выводить и любые тождества, содержащие также знаки «→», «~».Тождества V, VI, VII показывают, что константы И и Л, импликацию и эквиваленцию, рассматривая их как функции, можно выразить через конъюнкцию, дизъюнкцию и отрицание. Имеет место теорема, гласящая, что всякая функция алгебры логики может быть представлена через эти три операции, т.е. записана в виде выражения, содержащего лишь знаки этих операций и буквенные переменные. 

13. Используя таблицы двух аргументов, докажите тождество формул и

14) Приведите формулы представления чисел в позиционных системах счисления с основаниями 10 и 2.

Само число в произвольной p - ичной системе счисления (основание системы равно p) представляется в следующем виде

, (1)

при этом число изображается как последовательность цифр , т.е.

.

15)Приведите пример перевода по шагам целого числа из системы счисления с основанием 2 в систему счисления с основанием 10.

Переведем двоичное число 10001001 в десятичную систему счисления

Представим двоичное число в виде суммы степеней двойки с коэффициентами-цифрами и найдем эту сумму.

100010012 = 1* 2^7 +0* 2^6 + 0* 2^5 + 0* 2^4 + 1* 2^3 + 0* 2^2 + 0* 2^1 + 1* 2^0 = 128+8+1=13710

16)Приведите пример перевода по шагам целого числа из системы счисления с основанием 10 в систему счисления с основанием 2.

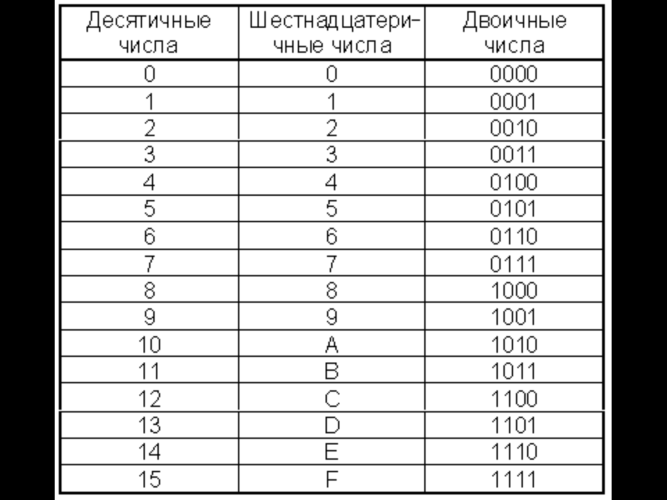
17) Приведите пример перевода по шагам целого числа из системы счисления с основанием 2 в систему счисления с основанием 16

Вводим двоичное число, разбиваем на тетрады (по 4 символа), и в соответствии каждой тетраде записываем число из шестнадцатиричной системы.

18) Какой смысл имеет минимальная единица информации? Какие единицы измерения информации используют в вычислительной технике? Во сколько раз один байт меньше одного килобайта?

В двоичной системе счисления в качестве минимальной единицы измерения информации принято такое ее количество, которое уменьшает неопределенность знания о состоянии источника в 2 раза. Такая единица носит выше название бит.

1 байт = 8 бит , 1 килобайт(кб)= 2¹⁰ , 1 мегабайт(мб)= 2²⁰ , 1 гигабайт (гб)= 2³⁰ , 1 терабайт (тб)= 2⁴⁰

Один байт в 128 раз меньше одного килобайта

19) Приведите пример перевода по шагам целого числа из системы счисления с основанием 16 в систему счисления с основанием 2.

20) Приведите определение алгоритма. Перечислите свойства алгоритмов и дайте пояснения к ним.

Алгоритм — точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время.

Алгоритм обладает следующими свойствами:

1. Дискретность. Это свойство состоит в том, что алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, т.е. преобразование исходных данных в результат осуществляется во времени дискретно.

2. Определенность. Каждое правило алгоритма должно быть четким, однозначным.

3. Результативность. Алгоритм должен приводить к решению за конечное число шагов.

4. Массовость. Алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными.

5. Правильность. Алгоритм правильный, если его выполнение дает правильные результаты решения поставленной задачи

21) Схемы алгоритмов: основные блоки и правила построения. Примеры схем алгоритмов с линейной, разветвляющейся и циклической структурой.

Блок-схема — распространенный тип схем (графических моделей), описывающих алгоритмы или процессы, в которых отдельные шаги изображаются в виде блоков различной формы, соединенных между собой линиями, указывающими направление последовательности.

Наименование	Обозначение	Функция
Блок начало-конец (пуск-остановка)		Элемент отображает вход из внешней среды или выход из неё (наиболее частое применение − начало и конец программы). Внутри фигуры записывается соответствующее действие.
Блок вычислений (вычислительный блок)		Выполнение одной или нескольких операций, обработка данных любого вида (изменение значения данных, формы представления, расположения). Внутри фигуры записывают непосредственно сами операции, например, операцию присваивания: a = 10*b + c.
Логический блок (блок условия)		Отображает решение или функцию переключательного типа с одним входом и двумя или более альтернативными выходами, из которых только один может быть выбран после вычисления условий, определенных внутри этого элемента. Вход в элемент обозначается линией, входящей обычно в верхнюю вершину элемента. Если выходов два или три, то обычно каждый выход обозначается линией, выходящей из оставшихся вершин (боковых и нижней). Если выходов больше трех, то их следует показывать одной линией, выходящей из вершины (чаще нижней) элемента, которая затем разветвляется. Соответствующие результаты вычислений могут записываться рядом с линиями, отображающими эти пути. Примеры решения: в общем случае − сравнение (три выхода: >, <, =); в программировании − условные операторы if (два выхода: true, false) и case (множество выходов).
Предопределённый процесс		Символ отображает выполнение процесса, состоящего из одной или нескольких операций, который определен в другом месте программы (в подпрограмме, модуле). Внутри символа записывается название процесса и передаваемые в него данные. Например, в программировании − вызов процедуры или функции.
Данные (ввод-вывод)		Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). Данный символ не определяет носителя данных (для указания типа носителя данных используются специфические символы).
Граница цикла		Символ состоит из двух частей − соответственно, начало и конец цикла − операции, выполняемые внутри цикла, размещаются между ними. Условия цикла и приращения записываются внутри символа начала или конца цикла − в зависимости от типа организации цикла. Часто для изображения на блок-схеме цикла вместо данного символа используют символ условия, указывая в нём решение, а одну из линий выхода замыкают выше в блок-схеме (перед операциями цикла).
Соединитель		Символ отображает вход в часть схемы и выход из другой части этой схемы. Используется для обрыва линии и продолжения её в другом месте (для избежания излишних пересечений или слишком длинных линий, а также, если схема состоит из нескольких страниц). Соответствующие соединительные символы должны иметь одинаковое (при том уникальное) обозначение.
Комментарий		Используется для более подробного описания шага, процесса или группы процессов. Описание помещается со стороны квадратной скобки и охватывается ей по всей высоте. Пунктирная линия идет к описываемому элементу, либо группе элементов (при этом группа выделяется замкнутой пунктирной линией). Также символ комментария следует использовать в тех случаях, когда объём текста, помещаемого внутри некоего символа (например, символ процесса, символ данных и др.), превышает размер самого этого символа.

Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.6).

Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 1.10 - 1.11.

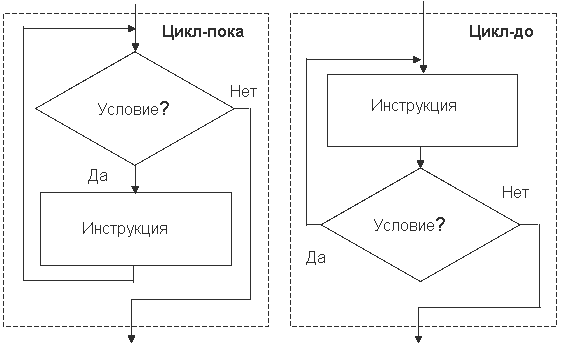
Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры

в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием - после тела цикла;

в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;

в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием - условие выхода из цикла.

Рис. 1.6 Размещение блоков в линейном алгоритме
Рис. 1.10 Фрагмент алгоритма	Рис. 1.11 Пример разветвления

22) Что понимают под вычислительной сложностью алгоритма? Приведите примеры задач, решаемых с помощью алгоритмов с квадратичной сложностью и экспоненциальной сложностью.

В информатике и теории алгоритмов вычислительная сложность алгоритма — это функция, определяющая зависимость объёма работы, выполняемой некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений.

Вычислительная сложность алгоритма - количество элементарных операций, затрачиваемых алгоритмом для решения конкретной задачи. Сложность зависит не только от размерности входных данных, но и от самих данных. Очевидно, что чем сложнее алгоритм в вычислительном плане, тем больше времени и вычислительных ресурсов потребует его выполнение.

Экспоненциальная сложность или экспоненциальное время — в теории сложности алгоритмов, время решения задачи, ограниченное экспонентой от размерности задачи. Другими словами, если размерность задачи возрастает линейно, время её решения возрастает экспоненциально

Сложность зависит не только от размерности входных данных, но и от самих данных. Очевидно, что чем сложнее алгоритм в вычислительном плане, тем больше времени и вычислительных ресурсов потребует его выполнение.Различают временную и пространственную сложность. Первая определяет время, требуемое на решение задачи заданной размерности с помощью данного алгоритма, а вторая - количество требуемых ресурсов (памяти) при тех же условиях.Каждый вычислительный алгоритм может быть отнесен к одному из двух классов сложности. В данном случае это множество задач, для решения которых известны алгоритмы, схожие по трудоемкости. В классе P вычислительные затраты линейно растут с увеличением размерности. Например, время, требуемое на уборку снега, прямо пропорционально площади. Если ее увеличить вдвое, то и временные затраты также возрастут в два раза. Класс NP включает задачи, для решения которых известны только алгоритмы, сложность которых экспоненциально зависит от размерности данных. Поэтому они, как правило, неэффективны при работе с большими множествами. Примером является задача поиска выхода из лабиринта, временные затраты на который экспоненциально растут с увеличением числа разветвлений.

23) Что понимают под емкостной сложностью алгоритма? Примеры.

Емкостная сложность алгоритма (Space complexity of an algorithm) - один из параметров, характеризующих алгоритм; определяется объемом памяти, использованным алгоритмом как функцией размера задачи.

24. Общая схема ЭВМ. Назначение и основные характеристики устройств. Принципы построения ЭВМ, сформулированные фон Нейманом.

Принципы фон Неймана:

Принцип однородности памяти : Программы и данные хранятся в одной и той же памяти. Поэтому ЭВМ не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.

Принцип адресуемости памяти: Основная память структурно состоит из пронумерованных ячеек; процессору в произвольный момент времени доступна любая ячейка. Отсюда следует возможность давать имена областям памяти, так, чтобы к хранящимся в них значениям можно было бы впоследствии обращаться или менять их в процессе выполнения программы с использованием присвоенных имен.

Принцип последовательного программного управления : Предполагает, что программа состоит из набора команд, которые выполняются процессором автоматически друг за другом в определенной последовательности.

Принцип жесткости архитектуры: Неизменяемость в процессе работы топологии, архитектуры, списка команд.

Так же в некоторых источниках указывается принцип двоичного кодирования, но существовали машины работающие с троичным и с десятичным кодом.

Основные устройства пк, их назначения и характеристики: 1. Микропроцессор 2. Внутренняя память 3. Контороллеры и адаптеры 4. Системная шина 5. Монитор 6. Клавиатура

В состав материнской платы входят такие основные компоненты:

Микропроцессор, оперативная память (ОЗУ), ПЗУ,видеокарта – для работы с графикой, звуковая карта, сетевая карта, контроллеры (адаптеры), порты;

Порт – средство для подключения периферийных устройств к материальной плате.

Магистраль – (системная шина) – это набор электронных линий, связывающих ЦП, основную память и периферийные устройства воедино, относительно передачи данных, служебных сигналов и адресации памяти.

  Основные принципы построения ЭВМ были сформулированы американским учёным Джоном фон Нейманом в 40-х годах 20 века:

1. Любую ЭВМ образуют три основные компоненты: процессор, память и устройства ввода-вывода (УВВ).

2. Информация, с которой работает ЭВМ делится на два типа:

• набор команд по обработке (программы);

• данные подлежащие обработке.

3. И команды, и данные вводятся в память (ОЗУ) – принцип хранимой программы.

4. Руководит обработкой процессор, устройство управления (УУ) которого выбирает команды из ОЗУ и организует их выполнение, а арифметико-логическое устройство (АЛУ) проводит арифметические и логические операции над данными.

5. С процессором и ОЗУ связаны устройства ввода-вывода (УВВ).

Архитектура современных персональных компьютеров основана на магистрально-модульном принципе. Информационная связь между устройствами компьютера осуществляется через системную шину (другое название - системная магистраль).

Шина - это кабель, состоящий из множества проводников. По одной группе проводников - шине данных передаётся обрабатываемая информация, по другой - шине адреса - адреса памяти или внешних устройств, к которым обращается процессор. Третья часть магистрали - шина управления, по ней передаются управляющие сигналы (например, сигнал готовности устройства к работе, сигнал к началу работы устройства и др).

Системная шина характеризуется тактовой частотой и разрядностью. Количество одновременно передаваемых по шине бит называется разрядностью шины. Тактовая частота характеризует число элементарных операций по передаче данных в 1 секунду. Разрядность шины измеряется в битах, тактовая частота – в мегагерцах.

Всякая информация, передаваемая от процессора к другим устройствам по шине данных, сопровождается адресом, передаваемым по адресной шине. Это может быть адрес ячейки памяти или адрес периферийного устройства. Необходимо, чтобы разрядность шины позволила передать адрес ячейки памяти. Таким образом, словами разрядность шины ограничивает объем оперативной памяти ЭВМ, он не может быть больше чем  , где n – разрядность шины. Важно, чтобы производительности всех подсоединённых к шине устройств были согласованы. Неразумно иметь быстрый процессор и медленную память или быстрый процессор и память, но медленный винчестер.

Ниже представлена схема устройства компьютера, построенного по магистральному принципу:

В современных ЭВМ реализован принцип открытой архитектуры, позволяющий пользователю самому комплектовать нужную ему конфигурацию компьютера и производить при необходимости её модернизацию. Конфигурацией компьютера называют фактический набор компонентов ЭВМ, которые составляют компьютер. Принцип открытой архитектуры позволяет менять состав устройств ЭВМ. К информационной магистрали могут подключаться дополнительные периферийные устройства, одни модели устройств могут заменяться на другие.

Аппаратное подключение периферийного устройства к магистрали на физическом уровне осуществляется через специальный блок - контроллер (другие названия - адаптер, плата, карта). Для установки контроллеров на материнской плате имеются специальные разъёмы - слоты.

24. Центральный процессор (ЦП). Назначение, характеристики, основные устройства процессора и их взаимодействие при выполнении машинных команд (на примерах команд сложения и условной передачи управления).

Центральный процессор - это центральное устройство компьютера, которое выполняет операции по обработке данных и управляет периферийными устройствами компьютера.

В состав центрального процессора входят:

• устройство управления (УУ);

• арифметико-логическое устройство (АЛУ);

• запоминающее устройство (ЗУ) на основе регистров процессорной памяти и кэш-памяти процессора;

• генератор тактовой частоты (ГТЧ).

К основным характеристикам процессора относятся:

• Быстродействие (вычислительная мощность) – это среднее число операций процессора в секунду.

• Тактовая частота в МГц. Тактовая равна количеству тактов в секунду. Такт - это промежуток времени между началом подачи текущего импульса ГТЧ и началом подачи следующего. г.). Как видно, увеличение частоты – одна из основных тенденций развития микропроцессоров.

• Разрядность процессора - это максимальное количество бит информации, которые могут обрабатываться и передаваться процессором одновременно. Разрядность процессора определяется разрядностью регистров, в которые помещаются обрабатываемые данные. Например, если регистр имеет разрядность 2 байта, то разрядность процессора равна 16 (2x8); если 4 байта, то 32; если 8 байтов, то 64

24. Оперативная и кэш память. Назначение и основные характеристики.

Оперативная память — устройство для хранения программ и дан­ных, которые обрабатываются процессором в текущем сеансе работы. Устройство оперативной памяти обеспечивает режимы запи­си, считывания и хранения информации, причем в любой мо­мент времени возможен доступ к любой ячейке памяти

Кэш-память (англ. cache — тайник, склад) служит для увели­чения производительности компьютера. «Секретность» кэша заключается в том, что он невидим для пользователя, и данные, хранящиеся там, недоступны для прикладного программного обеспечения. Кэш-память используется при обмене данными между микро­процессором и оперативной памятью. Алгоритм ее работы позво­ляет сократить частоту обращений микропроцессора к опера­тивной памяти и, следовательно, повысить производительность компьютера. кэш-память - область сверхоперативной памяти, выполненная на микросхемах статической памяти с временем доступа. Блок информации (программные конструкции, наборы данных) из оперативной памяти считывается сначала в кэш-память и уже из нее считывается процессором. Преимущество такого способа передачи данных заключается в том, что, во-первых, часть обращений к медленному ОЗУ заменяется на обращения к быстрой статической памяти, а во-вторых, информация из кэш-памяти поступает по быстродействующей шине.

27) Внешние запоминающие устройства (ВЗУ). Типы ВЗУ, основные характеристики.