1). Метод прямоугольников

В Методе прямоугольников непосредственно используется замена определенного интеграла интегральной суммой. В качестве точек x_i; могут выбираться левые (x_i-1) или правые (x_i) границы элементарных отрезков. Расчетные формулы можно записать так:

При выборе левых границ (см. рис.1)

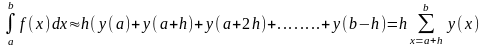
При выборе правых границ (см. рис.2)

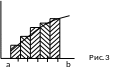
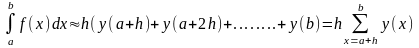
При выборе границ от a+ h/2 до b-h/2

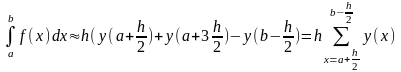
Рис.4

2) Метод трапеций

В методе трапеций график функции f(х) аппроксимируется ломаной, соединяющей точки с координатами (x_i, у)

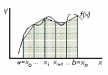
Рис.5

Искомое значение определенного интеграла представляется в виде суммы площадей трапеций, построенных на каждом из элементарных отрезков:

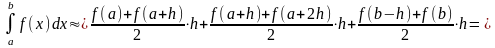
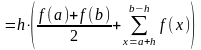
3) Метод парабол

В методе парабол (формула Симпсона) на каждом из элементарных отрезков по трем известным значениям функции f(Xj) строится парабола, заданная уравнением aх²+bх+с.

Формула для нахождения определенного интеграла может быть выведена из условия равенства значений: у_i = aх_i²+ bx_i +с:

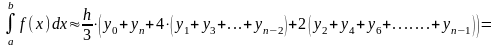
Уточнение корня уравнения

2. Основные теоретические положения

Многие задачи исследования различных объектов с помощью математических моделей, применяемых их для прогноза или расчёта, приводят к необходимости решения нелинейных уравнений.

Уравнения могут быть алгебраическими и трансцендентными. Пример

алгебраического уравнения: y = a + bx + cx², трансцендентного: y = eⁿ + x.

Решить уравнение – это найти такое значение переменной х, при котором заданная функция равна нулю (f (x) = 0).

Как правило, процесс решения нелинейного уравнения обще­го вида f(х)=0 осуществляется в два этапа. На первом этапе от­деляют корни, т.е. находят такие отрезки, внутри которых нахо­дится строго один корень. На втором этапе уточняют корень, т.е. находят его значение х* с предварительно заданной точностью ε. В практических задачах решением называют любое значение х, отличающееся по модулю от точного значения х* не более чем на величину ε.

1). Метод дихотомии

Пусть функция f (x) отрицательна в точке a (f (a) < 0), положительна в точке b (f (b) > 0), и непрерывна на отрезке [a, b] график функции пересекает ось Х, т. е. на этом отрезке имеется корень уравнения–точка,в-которой-f(х)= 0.

Тот же вывод следует, если f(а) > 0, f(b) < 0. В общем виде это формулируется так: в точках а и b функция f(х) принимает значения разных знаков. Если нам известен хотя бы один такой отрезок, пусть и большой длины, мы можем построить процедуру быстрого и сколь угодно точного поиска корня уравнения. Найдем значение функции в точке с, находящейся в середине отрезка: с =(a + b)/2. Знак f(с) совпадает со знаком функции на одном из концов отрезка и противоположен знаку функции на другом конце.

Пусть разные знаки f(х) в точках а и с. Значит на [а, с] наверняка есть искомый корень уравнения.

Таким образом, мы получили задачу, эквивалентную исходной, но теперь длина отрезка, на котором, как нам известно, находится корень, в два раза короче. Отрезок [а, с] опять можно разделить пополам и оставить в рассмотрении только один из двух получившихся (учитывая знаки значений f(х) на концах этих отрезков). Выбранный отрезок вновь разделить, и продолжать так до тех пор, пока отрезок, на котором находится корень, не станет достаточно мал.