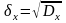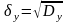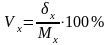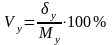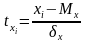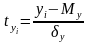1.Статистическая обработка экс. Математическая постановка задачи

(характеристики случайных величин)

3. Среднее квадратическое отклонение

по х:

по у:

Эта величина называется также стандартным отклонением, выражается в тех же единицах, что и величины, полученные в результате эксперимента. И зачастую оказывается более удобной характеристикой, чем дисперсия. Чем слабее варьирует признак, тем меньше среднее квадратическое отклонение.

4. Коэффициент вариации

Коэффициент вариации необходим для сравнения изменчивости признаков, выраженных разными единицами. Дисперсия и среднее квадратическое отклонение – величины абсолютные, именованные, выражаемые в тех же единицах, что и характеризуемый ими признак.

Коэффициент вариации – относительный показатель, представляет процентное отношение среднего квадратического отклонения к математическому ожиданию

по х:

по у:

5. Нормированное отклонение

Нормированное отклонение – показатель, представленный отклонением той или иной величиной от математического ожидания, отнесённое к величине среднего квадратического отклонения:

по х:

по у:

6. Коэффициент корреляции

Коэффициент корреляции характеризует степень линейной зависимости (степень связи) между величинами х и у.

Вычисляется по формуле:

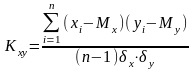
Или

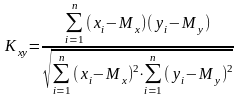
Значение К_ху изменяется в пределах от -1 до +1. Если значение К_ху > 0, то корреляция положительная (с ростом х значение у увеличивается), если К_ху < 0, то корреляция отрицательная (с ростом х значение у уменьшается).

При значении | К_ху | близком к 1 существует линейная зависимость между х и у, т.е. 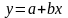, знак корреляции совпадает со знаком коэффициента .

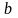Определение значимости коэффициента корреляции

Уровень значимости коэффициента корреляции может быть определён по критерию Стьюдента:

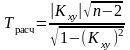
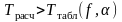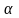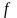Если , где - уровень значимости =0.95, а - число степеней свободы =n-2, то можно утверждать, что между х и у существует линейная зависимость, в противном случае – линейная зависимость отсутствует.

Значение T _табл выбирается по таблице значений критерия Стьюдента.

6.Численное интегрирование

2. Основные теоретические сведения.

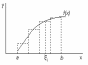
Пусть на отрезке [а,b] задана функция f(x). Определенный интеграл определяется как площадь, ограниченная подынтегральной функцией f(x), осью x и ординатами в точках «a» и «b»

Определенным интегралом от функции f(x) на отрезке [а, b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения.

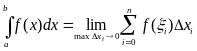
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной F(х) на отрезке интегрирования. На практике этой формулой часто нельзя воспользоваться по двум основным причинам:

Вид функции не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях

Значения функций f(х) заданы таблично (множество х_i конечно)

В этих случаях используются методы численного интегрирования.

Частным случаем в методах численного интегрирования является тот, когда величина элементарного отрезка ∆х,- величина постоянная и может быть вынесена за знак интегральной суммы. Эта величина называется шагом интегрирования и обозначается обычно ∆х.

Рассмотрим методы численного интегрирования.