19. Понятие функции полезности потребительской корзины

Потребители максимизируют удовлетворение, которого могут достичь при ограниченном бюд­жете. Когда потребитель максимизирует удовлетворение, потребляя каждый из двух товаров, предельная норма замещения равна соотношению цен этих двух приобретаемых товаров. Максимизация полезности может привести к "угловому" решению, если один из товаров не потребляется. В этом случае требование равенства предельной нормы замещения соотноше­нию цен не выполняется. Теория выявленных предпочтений показывает, как можно использовать информацию о выбо­ре человека при меняющихся ценах и доходе для определения его предпочтений. Если он выбирает потребительскую корзину Л, но может позволить себе и В, то потребительская кор­зина Л предпочтительнее потребительской корзины В. Теория потребительского выбора может быть представлена либо с помощью кривых без­различия, когда важны лишь порядковые характеристики полезности (которые позволяют ранжировать альтернативные потребительские корзины), либо с использованием функции полезности. Функция полезности строится путем присвоения численного значения каждой потребительской корзине. Если корзина А предпочтительнее корзины В, полезность А выше, чем полезность В.

Функция полезности, или функция благосостояния, потребителя — это выражение зависимости общего уровня полезности набора благ ( ) от объема потребления различных благ ( ), входящих в данный набор:  .

Потребительская корзина

На рынке потребитель сталкивается с бесчисленным количеством товаров и услуг, из которых он должен сформировать свою "потребительскую корзину", т.е. набор товаров, который обладает для него определенной полезностью. Это первое правило потребительского поведения.

Потребительская корзина — это совокупность товаров и услуг, выбранных покупателем и обладающая для потребителя определенным качеством. Каждой потребительской корзине соответствует некоторое число  , называемое совокупной полезностью.

Записывается потребительская корзина как:

где:   — количество товара;   — число товаров в экономике.

Потребительская корзина является основой для минимального потребительского бюджета, тогда под ней понимается не только набор товаров и услуг, объективно необходимых для удовлетворения первоочередных потребностей человека, но и оценка этого набора в действующих ценах.

Полезность, являющаяся целью потребления, представляет собой свойство экономических благ удовлетворять потребности, приносить удовольствие, удовлетворение от потребления.

20. Постановка задачи рыночного поведения потребителя. Примеры. Анализ поведения потребителя.

Рассмотрим модель поведения потребителя. Проблема, с которой потребитель сталкивается в рыночной экономике, состоит в том, чтобы выбрать такие уровни потребления различных товаров и услуг, которые были бы доступны для их покупки на рынке. Мы назовём эти товары и услуги благами. Для простоты предположим, что число благ конечно и равно N: n = 1, 2,…, N . Пространство благ, включающее в себя различные количества всевозможных товаров и услуг, будем обозначать R^N. Товарный, или потребительский, набор есть перечень количеств благ из данного пространства, которые индивид потребляет в течение определённого периода времени. Товарный набор может быть рассмотрен как точка в пространстве благ и обозначается следующим образом: x= (x₁, x₂, ... , x_n), где x_n - количество благ n (n = 1, 2,…, n). (1) Пусть, например, первое благо – это картофель, второе – молоко, третье – свинина. И наш потребитель в течение недели потребляет 3 кг картофеля, 5 л молока и 2 кг свинины, а всеми остальными товарами и услугами не пользуется. Тогда его товарный набор будет представлен так:  x = (3, 5, 2, 0,...,0). Таким образом, понятие товарного набора используется экономистами для того, чтобы представить уровни потребления индивида. Потребительское множество представляет собой все товарные наборы с неотрицательным количеством благ: 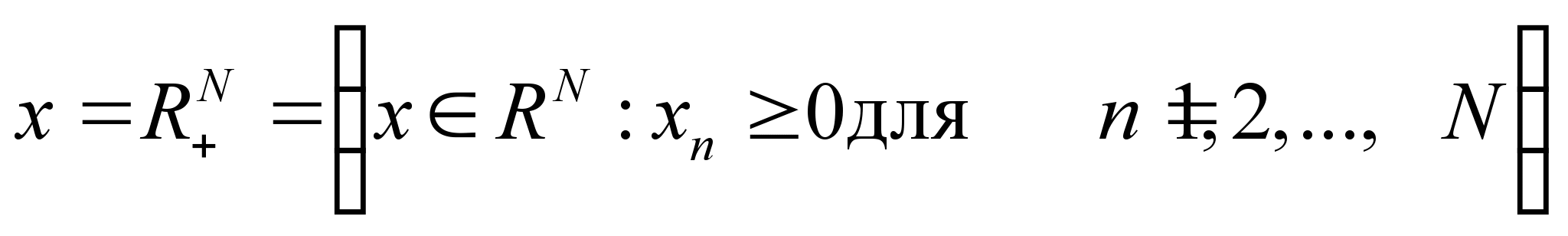 (2) Потребительское множество есть подмножество пространства благ, обозначаемое X ⊂ R^N , элементы которого являются такими товарными наборами, которые потребитель, в принципе, может потребить при физических ограничениях, заданных его окружающей средой. Употребляется термин «отношение предпочтения», которое обозначается символом  .  Пусть x, y – товарные наборы из потребительского множества X , где x=(x₁ , ..., x_n), y=(y₁ ,..., y_n). Тогда отношение x  y означает, что для рассматриваемого потребителя товарный набор xпредпочтительнее или, по меньшей мере, так же хорош, как набор y . Кроме того, выделяют отношение строго предпочтения (x   y) и отношение безразличия (x ~ y). Отношение строгого предпочтения означает, что набор x явно лучше для нашего потребителя, чем набор y. Отношение безразличия означает, что потребителю всё равно, какой товарный набор потребить x или y . Предпосылка о сравнимости утверждает, что индивид имеет чётко определённое отношение предпочтения между любыми двумя товарными наборами из потребительского множества: x, y X : или x y , или y x, или x ~ y . (3) Свойство транзитивности отношения предпочтения также является очень сильной предпосылкой и составляет сердцевину концепции рациональности индивида. Транзитивность означает, что x, y, z  X : если x y и y  z , тогда x   z . (4) Свойство рефлексивности отношения предпочтения подразумевает, что любой товарный набор, по крайней мере, не хуже самого себя:  x  X : x   x (5) Зачастую очень удобно предположить, что большее количество товаров потребитель предпочитает меньшему количеству тех же благ, то есть использовать предпосылку о ненасыщаемости. Эта предпосылка улавливается в таком свойстве отношения предпочтения, как строгая монотонность. Отношение предпочтения на потребительском множестве X является строго монотонным при выполнении следующего условия: если x > y, тогда x   y. (6) Эта предпосылка говорит о том, что потребителю лучше, когда он, по меньшей мере, всех, кроме одного, товаров потребляет в таком же количестве, но уж как минимум одно благо он потребляет в большем количестве. Заметим сразу, что предпосылка о ненасыщаемости хорошо работает до тех пор, пока мы имеем дело с благами, а не с антиблагами. Отношение предпочтения является строго выпуклым, если для товарных наборов x, y, z из потребительского множества X выполняется следующее: если y   x , z  x и y ≠ z, тогда α · y + (1−α )   z  y, где 0 <α <1. (7) Чтобы лучше понять данное свойство отношения предпочтения, используем для анализа аппарат кривых безразличия. ^ Кривая безразличия – это графическое представление множества безразличия, то есть множества потребительских наборов, которые для нашего потребителя описываются отношением безразличия. Предположим, что некий индивид живёт в мире двух благ, то есть он может потреблять только первое и второе благо. На оси абсцисс будем откладывать количество первого товара, а на оси ординат – количество второго товара. В принципе, кривая безразличия может иметь любой вид из тех, которые показаны на рисунках 13 итуация, представленная на рис. 13а удовлетворяет утверждению 7, то есть предпосылке о строгой выпуклости отношения предпочтения. Легко видеть, что в этом случае кривая безразличия является выпуклой вниз. В дальнейшем мы будем называть такие кривые безразличия просто выпуклыми. Кривая, представленная на рис. 13b, является выпуклой вверх. В дальнейшем мы будем называть такие кривые вогнутыми. Из графика, изображённого на втором рисунке, видно, что предпосылка о строгой выпуклости отношения предпочтения не выполнятся, так как α · y + (1 −α )· z   x . Кривая безразличия, представленная на рис. 13c, описывает выпуклое отношение предпочтения, но не строго выпуклое.

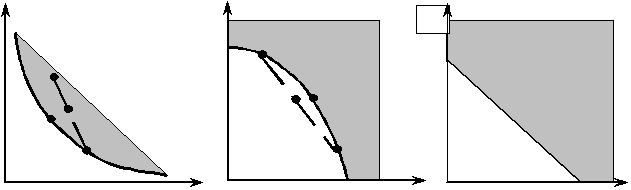
Рис.13