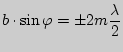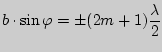Дифракция Фраунгофера Материал из Википедии — свободной энциклопедии

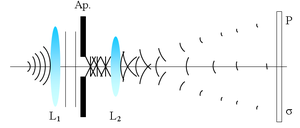
Пример оптической установки, в которой наблюдаются дифракция Френеля (в ближней зоне) и дифракция Фраунгофера (в дальней зоне).

Дифракция Френеля:

Дифракция Фраунгофера:

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, что бы можно было пренебречь в выражении для разности фаз членами порядка  , что сильно упрощает теоретическое рассмотрение явления. Здесь z — расстояние от отверстия или преграды до плоскости наблюдения, λ — длина волны излучения, а ρ — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля  , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).

[Править]Математическоe описание

В скалярной теории дифракция Фраунгофера определяется следующим интегралом:

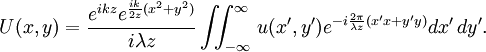
Дифракция на щели

Пусть плоская монохроматическая волна падает на экран с узкой бесконечно длинной щелью. На рис. 1   -- проекция экрана со щелью   на плоскость рисунка. Ширина щели ( ) имеет размер порядка длины волны света. Щель   вырезает часть фронта падающей световой волны. Все точки этого фронта колеблются в одинаковых фазах и на основании принципа Гюйгенса-Френеля, являются источниками вторичных волн.

Рис. 1 

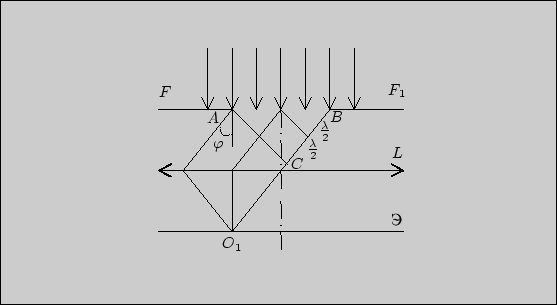
Рис. 2 

Вторичные волны распространяются по всем направлениям от (0) до (  ) к направлению распространения волн (рис. 1). Если за щелью поставить линзу, то все лучи, которые шли до линзы параллельно, соберутся в одной точке фокальной плоскости линзы. В этой точке наблюдается интерференция вторичных волн. Результат интерференции зависит от числа длин полуволн, которое укладывается в разности хода между соответствующими лучами.

Рассмотрим лучи, которые идут под некоторым углом   к направлению падающей световой волны (рис. 2).   -- разность хода между крайними лучами. Разобьем   на зоны Френеля (зоны Френеля в данном случае представляют собой систему параллельных плоскостей, перпендикулярных плоскости рисунка и построенных так, что расстояние от краев каждой зоны до точки   отличается на  ).

Если в   уложиться четное число длин полуволн, то в точке   будет ослабление света --  . Если нечетное, то усиление света --  . 

где m = 0; 1; 2; ...

Поскольку   (см. рис. 2), то эти условия можно записать в следующем виде: 

			(1)
			(2)

На рис. 3 дано распределение интенсивности света при дифракции на щели в зависимости от угла. Её можно вычислить по формуле: 

где		-	интенсивность в середине дифракционной картины;
		-	интенсивность в точке, определяемой значением.

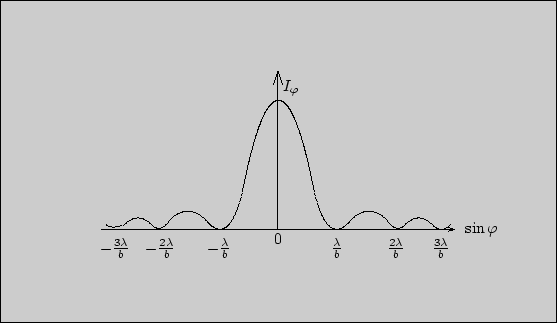
БИЛЕТ 26

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.

• Отражательные: Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отраженном свете

• Прозрачные: Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.

• Описание явления

• 

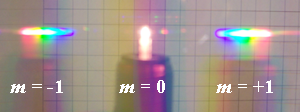
• Так выглядит свет лампы накаливания фонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m=0) соответствует свету, прошедшему сквозь решётку без отклонений. В силудисперсии решётки в первом (m=±1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному)

• Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для каждой длины волны существует свой угол дифракции, то белый свет раскладывается в спектр.

• Формулы

• Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.

• Если известно число штрихов (N), приходящихся на 1 мм решётки, то период решётки находят по формуле: 0,001 / N

• Формула дифракционной решётки:

• 

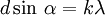
• где

• d — период решётки,

• α — угол максимума данного цвета,

• k — порядок максимума,

• λ — длина волны.

• Характеристики

• Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом φ для длины волны λ и под углом φ+Δφ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δφ/Δλ. Выражение для D можно получить если продифференцировать формулу дифракционной решётки

• 

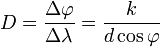
• Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра k.

• Изготовление

• 

• Нарезка компакт-диска может считаться дифракционной решёткой.

• Хорошие решётки требуют очень высокой точности изготовления. Если хоть одна щель из множества будет нанесена с ошибкой, то решётка будет бракована. Машина для изготовления решёток прочно и глубоко встраивается в специальный фундамент. Перед началом непосредственного изготовления решёток, машина работает 5-20 часов на холостом ходу для стабилизации всех своих узлов. Нарезание решётки длится до 7 суток, хотя время нанесения штриха составляет 2-3 секунды.

• Применение

• Дифракционную решётку применяют в спектральных приборах, также в качестве оптических датчиков линейных и угловых перемещений (измерительные дифракционные решётки), поляризаторов и фильтров инфракрасного излучения, делителей пучков в интерферометрах и так называемых "антибликовых" очках.

Диспе́рсия све́та (разложение света) — это явление зависимости абсолютного показателя преломления вещества от длины волны света (частотная дисперсия), а также, от координаты (пространственная дисперсия), или, что то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе —оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней:

• у красного цвета максимальная скорость в среде и минимальная степень преломления,

• у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления.

Однако в некоторых веществах (например в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.

Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.

• Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.

По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только кэлектромагнитной волне, но к любому волновому процессу.

Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).

Дисперсия является причиной хроматической аберрации — одного из тщательно устраняемых недостатков (аберраций) оптических систем, в том числе фотографических ивидео-объективов.

Коши пришел к формуле, выражающей зависимость показателя преломления от длины волны:

n = a + b / L² + c / L⁴ + …,

где:

• L — длина волны в вакууме;

• a, b, c, … — постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши.

Разрешающая способность (разрешающая сила) оптических приборов, характеризует способность этих приборов давать раздельные изображения двух близких друг к другу точек объекта. Наименьшее линейное или угловое расстояние между двумя точками, начиная с которого их изображения сливаются, называется линейным или угловым пределом разрешения. Обратная ему величина обычно служит количественной мерой Разрешающая способность (в оптике) Вследствие дифракции света на краях оптических деталей даже в идеальной оптической системе (т. е. безаберрационной; см. Аберрации оптических систем) изображение точки есть не точка, а кружок с центральным светлым пятном, окруженным кольцами (попеременно тёмными и светлыми вмонохроматическом свете, радужно окрашенными - в белом свете). Теория дифракции позволяет вычислить наименьшее расстояние, разрешаемое системой, если известно, при каких распределениях освещённости приёмник (глаз, фотослой) воспринимает изображения раздельно. Согласно Рэлею (1879), изображения двух точек одинаковой яркости ещё можно видеть раздельно, если центр дифракционного пятна каждого из них пересекается краем 1-го тёмного кольца другого (рис.). В случае самосветящихся точек, испускающих некогерентные лучи, при выполнении этого критерия Рэлея наименьшая освещённость между изображениями разрешаемых точек составит 74% своего максимального значения, а угловое расстояние между центрами дифракционных пятен (максимумами освещённости) Dj = 1,21 lID, где l - длина волны света, D - диаметр входного зрачка оптической системы (см.Диафрагма в оптике). Если f - фокусное расстояние оптической системы, то линейная величина рэлеевского предела разрешения s =1,21 lflD. Предел разрешения телескопов и зрительных труб выражают в угловых секундах (см. Разрешающая сила телескопа), для длины волны l @ 560 нм, соответствующей максимальной чувствительности человеческого глаза, он равен a"= 140/D (D в мм). Для фотообъективов Разрешающая способность (в оптике) обычно определяют как максимальное количество раздельно видимых линий на 1 мм изображения стандартного тест-объекта (см. Мира) и вычисляют по формуле N = 1470e, где e - относительное отверстие объектива (см. также Разрешающая способность фотографирующей системы; о Разрешающая способность (в оптике)микроскопов см. в ст. Микроскоп). Приведённые соотношения справедливы лишь для точек, находящихся на оси идеальной оптической системы. Наличие аберраций и погрешностей изготовления увеличивает размеры дифракционных пятен и снижаетРазрешающая способность (в оптике) реальных систем, которая, кроме того, уменьшается по мере удаления от центра поля зрения. Разрешающая способность (в оптике) оптического прибора R_oп, в состав которого входят оптическая система сРазрешающая способность (в оптике) R_oc и приёмник света (фотослой, катод электроннооптического преобразователя и пр.) сРазрешающая способность (в оптике) R_п, определяется приближённой формулой 1/R_oп = 1/R_oc + 1/R_п, из неё следует, что целесообразно использовать лишь сочетания, в которых R_oc и R_п - величины одного порядка. Разрешающая способность (в оптике) прибора может быть оценена по его аппаратной функции, отражающей все факторы, влияющие на качество изображения (дифракцию, аберрации и т.д.). Наряду с оценкой качества изображения по Разрешающая способность (в оптике) широко распространён метод его оценки с помощью частотно-контрастной характеристики. О Разрешающая способность (в оптике)спектральных приборов см. в ст. Спектральные приборы.     Лит.: Тудоровский А. И., Теория оптических приборов, 2 изд., ч. 1, М. - Л., 1948; Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Волосов Д. С., Фотографическая оптика, М., 1971.   Л. Н. Капорский.

БИЛЕТ 27

Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения. Наряду с рассеянием без изменения длины волны наблюдается рассеяние с изменением длины волны — так называемое комптоновское рассеяние (см. Комптона эффект). Явление Д. р. л., доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912.

  Кристалл является естественной трёхмерной дифракционной решёткой для рентгеновских лучей, т.к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (~1Å=10^-8 см). Д. р. л. на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллической решётки (см. Брэгга — Вульфа условие). Направление дифракционных максимумов удовлетворяет одновременно трём условиям:

  a (cos  — cos ₀) = Н,

  b (cos  — cos ₀) = K,

  с (cos  — cos ₀) = L.

Здесь а, b, с — периоды кристаллической решётки по трём её осям; ₀, ₀, ₀ — углы, образуемые падающим, а , ,  — рассеянным лучами с осями кристалла;  — длина волны рентгеновских лучей, Н, К, L — целые числа. Эти уравнения называются уравнениями Лауэ. Дифракционную картину получают либо от неподвижного кристалла с помощью рентгеновского излучения со сплошным спектром (так называемая лауэграмма; рис. 1), либо от вращающегося или колеблющегося кристалла (углы₀, ₀ меняются, а ₀ остаётся постоянным), освещаемого монохроматическим рентгеновским излучением ( — постоянно), либо от поликристалла, освещаемого монохроматическим излучением. В последнем случае, благодаря тому что отдельные кристаллы в образце ориентированы произвольно, меняются углы ₀, ₀, ₀.

  Интенсивность дифрагированного луча зависит в первую очередь от так называемого структурного фактора, который определяется атомными факторами атомов кристалла, их расположением внутри элементарной ячейки кристалла, а также характером тепловых колебаний атомов. Структурный фактор зависит от симметрии расположения атомов в элементарной ячейке. Интенсивность дифрагированного луча зависит также от размеров и формы объекта, от совершенства кристалла и прочего.

  Д. р. л. от поликристаллических тел приводит к возникновению резко выраженных конусов вторичных лучей. Осью конуса является первичный луч, а угол раствора конуса равен 4 ( — угол между отражающей плоскостью и падающим лучом). Каждый конус соответствует определённому семейству кристаллических плоскостей. В создании конуса участвуют все кристаллики, семейство плоскостей которых расположено под углом  к падающему лучу. Если кристаллики малы и их приходится очень большое количество на единицу объёма, то конус лучей будет сплошным. В случае текстуры, т. е. наличия предпочтительной ориентировки кристалликов, дифракционная картина (рентгенограмма) будет состоять из неравномерно зачернённых колец (см. также Дебая — Шеррера метод).

  Метод Д. р. л. на кристаллах дал возможность определять длину волны рентгеновских лучей, если известна структура кристаллической решётки, благодаря чему возникла рентгеновская спектроскопия, сыгравшая важную роль при установлении строения атома. Наблюдения Д. р. л. известной длины волны на кристалле неизвестной структуры позволяют установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл), что послужило основойрентгеновского структурного анализа.

  Д. р. л. наблюдается также при рассеянии их аморфными твёрдыми телами, жидкостями и газами. В этом случае на кривой зависимости интенсивности от угла рассеяния вокруг центрального пятна появляются широкие кольца типа гало (рис. 2). Положение этих колец (угол ) определяется средним расстоянием между молекулами или расстояниями между атомами в молекуле. Из зависимости интенсивности от угла рассеяния можно определить распределение плотности вещества.

  Д. р. л. можно наблюдать также на обычной оптической дифракционной решётке при скользящем падении (меньше угла полного отражения) рентгеновских лучей на решётку. С помощью этого метода можно непосредственно и с большой точностью измерять длины волн рентгеновских лучей.

Пусть две дифракционные решетки поставлены одна за другой так, что их штрихи взаимно перпендикулярны . Такая пластинка представляет собой двумерную периодическую структуру.

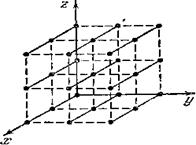
Рис. 5.11.1

Дифракция наблюдается также на трехмерных структурах, т. е. пространственных образованиях, обнаружи вающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами яв ляются все кристаллические тела. Однако период их (~ мк) слишком мал для того, чтобы можно было наблюдать дифракцию в види мом свете. Условие  , выполняется в случае кристаллов лишь для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ.

Найдем условия образования дифракционных максимумов от трехмерной структуры. Проведем в направлениях , по которым свойства структуры обнаруживают периодичность, координатные оси x, y, z (рис. 5.11.1). Структуру можно представить как совокупность равноотстоящих параллельных линейных цепочек из структурных элементов , расположенных вдоль одной из координатных осей . Рассмотрим действие отдельной линейной цепочки , параллельной , например ,  оси  х (рис. 5.11.2). Пусть на нее падает пучок параллельных лучей , образующих с осью  х угол  .Каждый структурный элемент является источником вторичных волн. К соседним источникам падающая волна приходит с разностью фаз  ,где    (  - период структуры вдоль оси х ). Кроме того между вторичными волнами , распространяющихся в направлениях, образующих с осью х угол   ( все такие направления лежат вдоль образующих конуса, осью которого служит ось х ), возникает дополнительная разность хода 

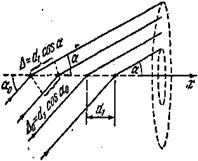
Рис. 5.11.2

Под действием рентгеновского излучения каждый атом кристаллической решетки становится источником сферических волн той же частоты, что и падающих волн. Запишем условия Лауэ ., ., , -угол между падающим пучком и осью y,  -угол, образуемый с осью yнаправлениями, вдоль которых получаются дифракционные максимумы. Уравнения  носят название формул Лауэ. Каждому определяемому этими уравнениями направлению( ) соответствуют три целочисленных индекса   и   ,   . При рассмотрении дифракции от трехмерной структуры мы не касались вопроса о том, каким образом лучи, идущие от различных  структурных элементов, сводятся в одну точку экрана. В случае дифракции, наблюдаемой в видимом свете, это, как мы знаем, достигается с помощью линзы, в фокальной плоскости которой расположен экран.. Русский ученый Ю. В. Вульф и английские физики У. Г. и У. Л. Брэгги показали независимо друг от друга, что расчет дифракционной картины от кристаллической

Рис. 5.11.3.

решетки можно провести также следующим простым способом.

Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.5.11.3.). В дальнейшем мы будем называть их атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычным законам отражения. Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различ ными щелями дифракционной решетки. При этом, как и  в случае решетки, вторичные волны  будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной  .  Из рис. 5.  видно, что разность хода двух волн,  отразившихся от соседних атомных слоев, равна  ,  где d - период идентичности кристалла в направлении, перпендикулярном к рассматриваемым  слоям,  - угол, дополнительный к углу падения и называемый углом скольжения падающих лучей. Следовательно, направления, в которых получаются дифракционные максимумы, определяются условием:

Соотношение называется формулой Вульфа - Брэгга.

Заметим, что расчет по формулам Лауэ и расчет по формуле Вульфа - Брэгга приводят к совпадающим результатам.

БИЛЕТ 28