Интеграл Френеля

Распределение электрического поля дифрагирующего света в точке (x,y,z) задаётся выражением

где  ,   — мнимая единица, и   — косинус угла между направлениями z и r. В аналитическом виде этот интеграл представим, только для простейших геометрий отверстий, поэтому он вычисляется обычно численными методами.

Аппроксимация Френеля

Главная трудность при вычислении интеграла представляет собой выражение для r. Во-первых, упростим вычисления сделав замену переменных:

Подставляя это выражение вместо r, найдём:

Воспользуемся разложением Тейлора в ряд

и выразим r в виде

Если мы рассмотрим все члены разложения это будет точным выраженим.^[1]. Подставим это выражение в аргумент экспоненциальной функции под интегралом; ключевую роль в приближениии Френеля играет пренебрежение третьего члена в разложении, который предполагается малым. Чтобы это было возможным, он должен слабо влиять на показатель степени. Другими словами, он должен быть намного меньше чем период показатель экспоненты, то есть 2π:

Выражая k в терминах длины волны,

получим следующее соотношение:

Умножая обе стороны на z / λ, получим

или, подставляя ранее полученное выражение для ρ²,

Если это услови выполняется для всех значений x, x' , y и y' , тогда мы можем пренебречь третьим членом в разложении Тейлора. Более того, если третий член мал, то все последующие слагаемые более высоких порядков тоже малы и ими можно пренебречь. Тогда можно аппроксимировать выражение используя два члена разложения:

Это выражение называется приближением Френеля, а неравенство полученное ранее есть условие применимости этого приближения.

Дифракция Френеля

Условие применимости достаточно слабо, и позволяет все характерные размеры взять как сравнимые величины, если апертура много меньше, чем длина пути. К тому же так как нас интересует только малая область недалеко от осточника величины x и y много меньше чем z, предположим  , что означает   и r в знаменателе можно аппроксимировать выражением  .

В противоположность дифракции Фраунгофера, дифракция Френеля должна учитывать кривизну волнового фронта, для того чтобы правильно учесть относительные фазыинтерферирующих волн.

Электрическое поле для дифракции Френеля в точке (x,y,z) дано в виде:

Это - интеграл дифракции Френеля; он означает, что, если приближение Френеля действительно, распространяющееся поле - сферическая^{[источник не указан 22 дня]} волна, начинающаяся в апертуре и движущаяся вдоль z. Интеграл модулирует амплитуду и фазу сферической волны. Аналитическое решение этого выражения возможно только в редких случаях. Для дальнейшего упрощения, действительного только для намного больших расстояний от источника дифракции, см. дифракция Фраунгофера.

Дифракция света Дифракция Френеля на круглом отверстии

 

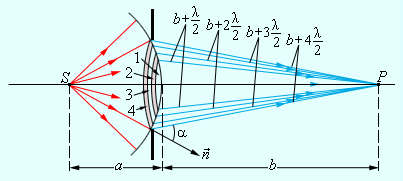
Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r₀. Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.

При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.

Можно показать, что радиус зоны Френеля с номером m при не очень больших m:

.

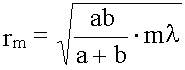Расстояние "a" примерно равно расстоянию от источника до преграды, расстояние "b" - от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля, то, приравняв r₀ и r_m, получим формулу для подсчета числа открытых зон Френеля:

.

При m четном в точке P будет минимум интенсивности, при нечетном - максимум.

При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна 

или A = A_m + 1 / 2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то A_m + 1 ≈ 2A₀ и A ≈ A₀, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.

Оценим размеры зон Френеля. Пусть, например, дифракционная картина наблюдается на экране, расположенном на расстоянии L = 1 м от препятствия. Длина волны света λ = 600 нм (красный свет). Тогда радиус первой зоны Френеля есть 

Таким образом, в оптическом диапазоне вследствие малости длины волны размер зон Френеля оказывается достаточно малым. Дифракционные явления проявляются наиболее отчетливо, когда на препятствии укладывается лишь небольшое число зон: 

Это соотношение можно рассматривать как критерий наблюдения дифракции. Если число зон Френеля, укладывающихся на препятствии, становится очень большим, дифракционные явления практически незаметны: 

Это сильное неравенство определяет границу применимости геометрической оптики. Узкий пучок света, который в геометрической оптике называется лучом, может быть сформирован только при выполнении этого условия. Таким образом, геометрическая оптика является предельным случаем волновой оптики.

Выше был рассмотрен случай дифракции света от удаленного источника на препятствиях круглой формы. Если точечный источник света находится на конечном расстоянии, то на препятствие падает сферически расходящаяся волна. В этом случае геометрия задачи несколько усложняется, так как зоны Френеля теперь нужно строить не на плоской, а на сферической поверхности (рис. 3.8.4).

Рисунок 3.8.4. Зоны Френеля на сферическом фронте волны.

Расчет приводит к следующему выражению для радиусов ρ_m зон Френеля на сферическом фронте волны: 

Все выводы изложенной выше теории Френеля остаются справедливыми и в этом случае.

Следует отметить, что теория дифракции (и интерференции) световых волн применима к волнам любой физической природы. В этом проявляется общность волновых закономерностей. Физическая природа света в начале XIX века, когда Т. Юнг, О. Френель и другие ученые развивали волновые представления, еще не была известна.

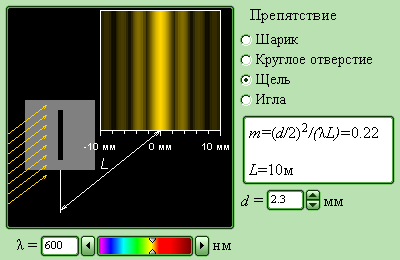
Модель. Дифракция света.

БИЛЕТ 25