Принцип Гюйгенса — Френеля Материал из Википедии — свободной энциклопедии

(Перенаправлено с Принцип Гюйгенса-Френеля)

Рефракция волн по Гюйгенсу

Дифракция волн по Гюйгенсу

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых.

Принцип Гюйгенса — Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится волновой поверхностью в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Г. Кирхгоф придал принципу Гюйгенса — Френеля строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа (см. метод Кирхгофа).

Фронтом волны точечного источника в однородном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Зоны Френеля, участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (или звука). Впервые этот метод применил О. Френель в 1815—19. Суть метода такова. Пусть от светящейся точки Q (рис.) распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке Р. Разделим поверхность волны S на кольцевые зоны; для этого проведём из точки Р сферы радиусами PO, Pa= PO + ^/₂; Pb = Pa + ^/₂, Pc = Pb + ^/₂, (О — точка пересечения поверхности волны с линией PQ;  — длина световой волны). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется З. Ф. Волновой процесс в точке Р можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой З. Ф. в отдельности. Амплитуда таких колебаний медленно убывает с возрастанием номера зоны (отсчитываемого от точки О), а фазы колебаний, вызываемых в Р смежными зонами, противоположны. Поэтому волны, приходящие в Р от двух смежных зон, гасят друг друга, а действие зон, следующих через одну, складывается. Если волна распространяется, не встречая препятствий, то, как показывает расчёт, её действие (сумма воздействий всех З. Ф.) эквивалентно действию половины первой зоны. Если же при помощи экрана с прозрачными концентрическими участками выделить части волны, соответствующие, например, N нечётным зонам Френеля, то действие всех выделенных зон сложится и амплитуда колебаний U_нечёт в точке Р возрастёт в 2N раз, а интенсивность света в 4N² раз, причём освещённость в точках, окружающих Р, уменьшится. То же получится при выделении только чётных зон, но фаза суммарной волны U_чёт будет иметь противоположный знак.

  Такие зонные экраны (т. н. линзы Френеля) находят применение не только в оптике, но и в акустике и радиотехнике — в области достаточно малых длин волн, когда размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).

  Метод З. Ф. позволяет быстро и наглядно составлять качественное, а иногда и довольно точное количественное представление о результате дифракции волн при различных сложных условиях их распространения. Он применяется поэтому не только в оптике, но и при изучении распространения радио- и звуковых волн для определения эффективной трассы «луча», идущего от передатчика к приёмнику; для выяснения того, будут ли при данных условиях играть роль дифракционные явления; для ориентировки в вопросах о направленности излучения, фокусировке волн и т.п.

Если между глазом и каким-нибудь источником света поместить непрозрачный предмет, то источник света мы не увидим. Объясняется это тем, что в однородной среде свет распространяется по прямым линиям. Прямолинейное распространение света — факт, установленный ещё в глубокой древности. Об этом писал основатель геометрии Евклид (300 лет до нашей эры). Прямолинейностью распространения света в однородной среде о бъясняется образование тени. Тени людей, деревьев, зданий и других предметов хорошо наблюдаются на земле в солнечный день.

Предметы, освещаемые точечными источниками света, например солнцем, отбрасывают четко очерченные тени. Карманный фонарик даёт узкий пучек света. Фактически о положении окружающих нас предметов в пространстве мы судим, подразумевая, что свет от обьекта попадает в наш глаз по прямолинейным траекториям. Наша ориентация во внешнем мире целиком основана на предположении о прямолинейном распространении света.

Именно это допущение привело к представлению о световых лучах.

Световой луч - это прямая, вдоль которой распространяется свет. Условно лучомн азывают узкий пучок света. Если мы видим предмет, то это означает, что нам в глаз попадает свет от каждой точки предмета. Хотя световые лучи выходят из каждой точки по всем направлениям, лишь узкий пучек этих лучей попадает в глаз наблюдателя. Если наблюдатель сдвинет голову чуть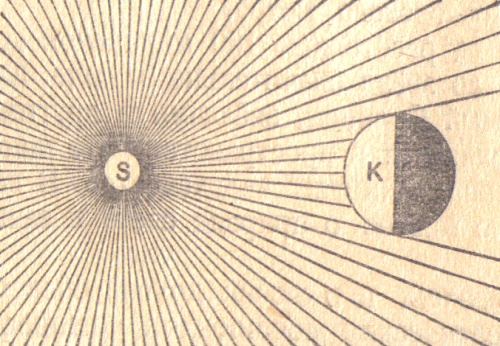 в сторону, то в его глаз от каждой точки предмета будет попадать уже другой пучек лучей.

На рисунке показана тень, полученная на экране при освещении точечным источником света S непрозрачного шара М. Так как шар непрозрачен, то он не пропускает свет, падающий на него; в результате на экране образуется тень. Такую тень можно получить в тёмной комнате, освещая шар карманным фонарём. Е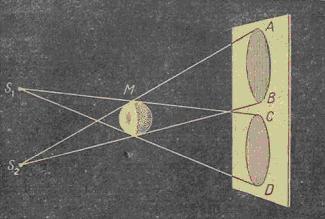 сли шар осветить двумя фонарями, то можно получить две тени и менее тёмные, чем тень от одного фонаря, так как тень освещена одним фонарём, а другая тень— вторым фонарем . Частично освещенные  участки  экрана    и  называются полутенями. Можно так расположить два источника света, что обе полутени будут частично перекрывать друг друга и часть поверхности экрана окажется совершенно неосвещённой. Это полная тень.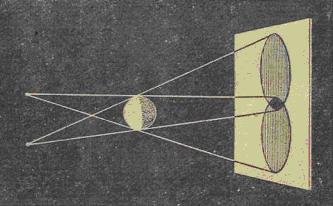

Закон прямолинейного распространения света : в однородной прозрачной среде свет распространяется прямолинейно.

Доказательством этого закона является образование тени и полутени.

БИЛЕТ 24

Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

На рисунке справа схематично изображён непрозрачный экран с круглым отверстием (апертура), слева от которого расположен источник света.Изображение фиксируется в другом экране справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затенена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друг друга, или гасятся в зависимости от разницы хода.