12. Регулярный режим охлаждения (нагревания) тел.

Анализ полученных решений для тел различной геометрической формы показывает, что все они имеют одинаковую структуру - ∑ ∞-го ряда, члены которой расположены по быстро убывающим экспоненциальным ф-циям. Например, для пластины:

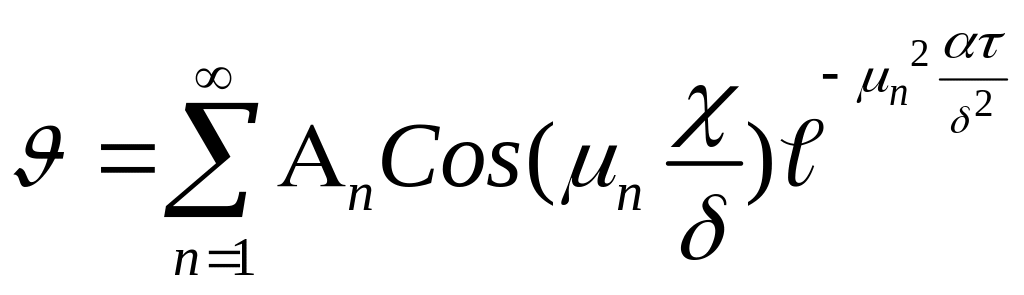
- ф-цией только координаты X.

Величина экспоненты будет убывать пропорционально времени τ.

Комплекс представляет собой постоянно положительное число, которое можно обозначить .

С учётом этого, выражение для пластины можно представить

(1)

Для тел других форм температурное поле также будет описываться уравнением этого же вида. Специфика геометрии учитывается различным видом множителей и .

I стадия II стадия

x=0

x=1

0 τ

При малых значениях τ от τ=0 до τ= распределение температуры тела и скорость изменения температуры во времени в отдельных точках тела зависят от особенностей начального распределения температуры.

В этих условиях поле температур в теле будет определятся не только первым, но и последующими членами ряда. Этот первый период охлаждения, при котором скорость изменения температур внутри тела зависит от вида начального распределения температур, называют неупорядоченной стадией охлаждения (нагрева). Благодаря с увеличением τ последующие члены ряда будут быстро убывать т.е. ряд становится быстросходящимся.

Начиная с некоторого , начальные условия начинают играть возрастающую роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами.

Температурное поле описывается первым членом ряда, т.е.

(2) (регулярный режим)

Это соотношение показывает, что относительное изменение температур, как в пространстве, так и во времени теперь не зависит от начального распределения температур. Логарифмируя:

или

(3) – графически зависимость – линейная.

При длительном охлаждении ( или ) все точки тела принимают одинаковую температуру равную , (наступило стационарное состояние) т.е. весь процесс охлаждения можно разделить на три стадии:

1. Неупорядоченый режим, характеризуется большим влиянием начального распределения температуры. Уравнение (1)

2. Регулярный режим (2)

3. Соответствует стационарному режиму ( )

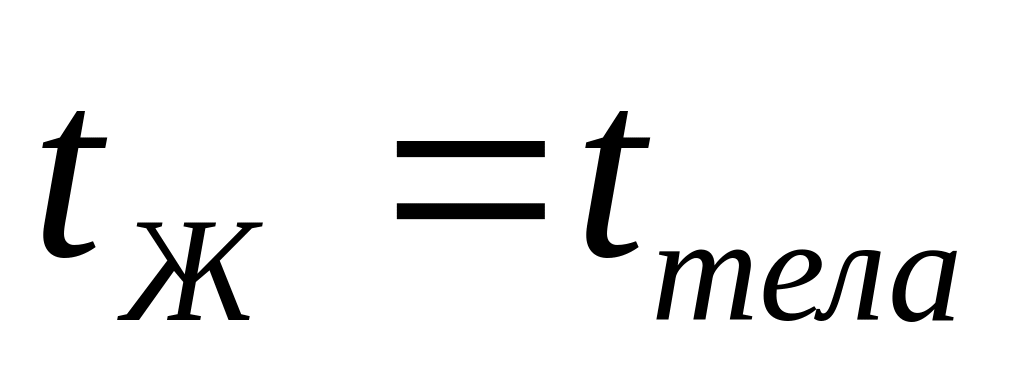Остановимся на регулярном режиме. После дифференцирования обеих частей уравнения (3) по времени, получим:

- относительная скорость изменения температуры

- темп охлаждения

При наступлении регулярного режима m не зависит ни от координат, ни от времени и является величиной постоянной для всех точек тела. m характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.

m находится как тангенс угла наклона прямой в стадии регулярного режима:

Зависимость m от физических и геометрических свойств тела можно найти из анализа уравнения теплового баланса.

Изменение внутренней энергии или энтальпии.

-средняя по объёму температура тела.

С другой стороны это же тепло должно быть отведено за счёт теплоотдачи:

-средняя температура поверхности тела в данный момент времени.

Приравнивая, получим:

после преобразования:

- полная теплоёмкость тела

m - пропорционально α и обратно пропорционально полной его теплоёмкости. Это первая теорема Кондратьева.

ψ – коэффициент равномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела.

а) (практически ) и (рис. а)

б) ( )

- x x - x x

В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное и равное температуре окружающей среды значение (рис. б)

Из этого следует, что 0<ψ<1.

При или m становится прямо пропорциональным коэффициенту температуропроводности тела а (2-я теорема Кондратьева)

k зависит только от геометрической формы и размеров тела

для безграничной пластины.

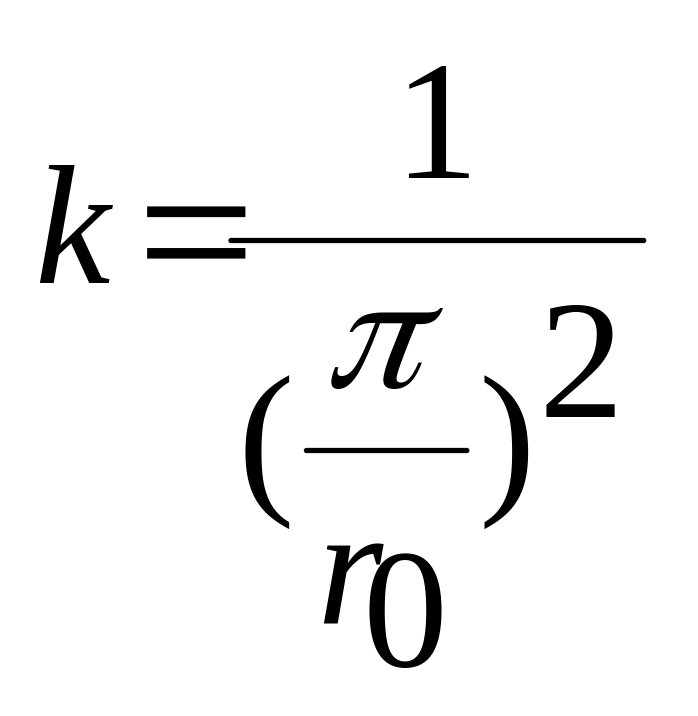для шара

для параллелепипеда

для цилиндра конечной длинны