33.Основные правила дифференцирования. Производная сложной функции, производная обратной функции. Производная неявно заданной функции. Производная функции, заданной параметрически.

Основные правила дифференцирования: Пусть f(x) = u, g(x) = v - функции, дифференцируемые в точке х.

1) (u ± v)′ = u′ ± v′ ;

Док-во:

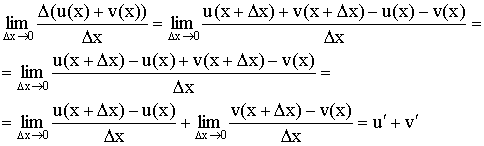
2) Постоянный множитель выносится за знак производной:

3) Производная произведения:

Док-во:

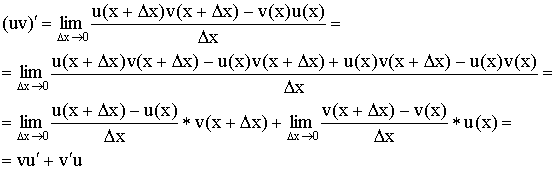
4) Производная дроби:

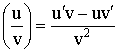
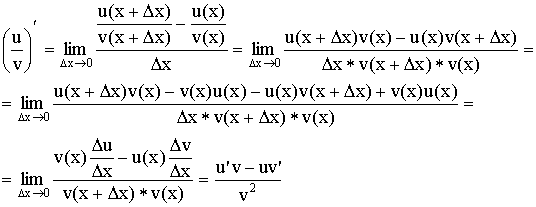
Производная сложной функции:

Пусть , определена и непрерывна в окрестности точки (u₀), определена и непрерывна в окрестности точки x₀. Тогда

Док-во:

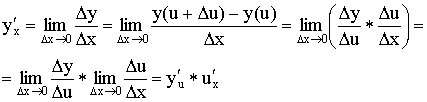
Производная обратной функции:

Пусть дифференцируемая в точке х₀. - обратная к .

Обратная функция существует, если монотонная функция. Тогда

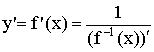
Док-во:

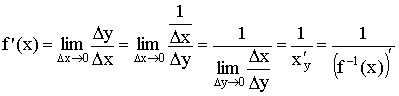
Производная неявно заданной функции:

– общий вид неявно заданной функции.

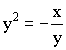
Док-во:

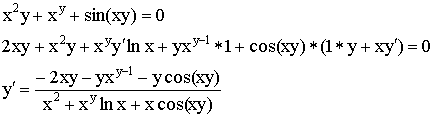
Производная функции, заданной параметрически:

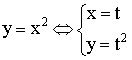
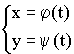
– дифференцируемы.

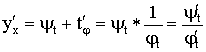
34.Связь между непрерывностью и дифференцируемостью функции.

Если функция дифференцируема в точке, то она в этой точке непрерывна.

Пример:

y =

y = x₁x > 0

-x₁x ≤ 0;

Этот пример показывает, что из непрерывности функции в точке, не следует её дифференцируемость.

35.Теоремы о дифференцируемых функциях (Ролля, Лагранжа, Коши, Лопиталя)

Теорема Ролля: Пусть ф-я y=f(х) непрерывна на отрезке [a;b] и иффер. на интервале (a;b). Если f(a)=f(b), то сущ. Одна (.) с € (a;b), такая, что f’(c)=0.

Геометрическая интерпретация :

С

У=f(a)

Док-во: Ф-я f(x) достигает на отрезке [a;b] своих наименьшего m и наибольшего M значения. Рассмотрим 2 случая:

1) m=M f(x)=с для любых с принадл [a;b].f'(x)=0 для любых х принадл[a;b].

2) m<M, тогда хотя бы одно из знач m или M принимается внутри интервала (a;b).

Пусть для определенности f(x0)=M, где х0 принадл (a;b), тогда х0-т. max, f'(x0)=0

Теорема Коши: пусть ф-ции f(x) и g(x) непрерывны на [a;b ]и диффер на (a;b), g'(x)≠0 для любых x принадл(a;b), тогда найдется хотя бы одна С принадл (a;b) такая, что (f(b)-f(a))/(g(b)-g(a))=f'(С)/g'(С).

Док-во: Замечая, что g(b)≠g(a), иначе для g(x) выполнялись бы все условия т.Ролля и нашлась бы т.С принадл (a;b) такая, что g'(C)=0

Рассмотрим вспомогательную ф-цию Покажем, что y(x) удовл усл т.Ролля. Действительно y(x) непрерывна на [a;b ]и диффер на (a;b). Ввиду непрерывности и диффренцир на них f(x) и g(x).

По т. Ролля сущ. С принадл (a;b) такая, что y'(С)=0

, следов

Теорема Лагранжа: пусть ф-ция f(x) непрерывн на [a;b ]и диффер на (a;b), тогда найдется хотя бы одна С принадл (a;b) такая, что f(b)-f(a)= f'(C)(b-a).

Док-во вытекает из т.Ролля для g(x)=1 для любых х принадл [a;b ]

Правило Лопиталя. Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при ха равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Доказательство. Применив формулу Коши, получим:

где  - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:

Пусть при ха отношение стремится к некоторому пределу. Т.к. точка  лежит между точками а и х, то при ха получим а, а следовательно и отношение стремится к тому же пределу. Таким образом, можно записать:

.

Теорема доказана.

Неопределенности вида можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида , f(x)>0 вблизи точки а при ха. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).